Механизм образования себестоимости продукции

Предположим, что для производства одной единицы (валовой) продукции 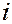–й отрасли необходимо затратить единиц –го сырья, . Сырье понимается в широком смысле слова: закупаемые материалы, электроэнергия, производственные фонды, труд и т.д.

Обозначим -матрицу удельных коэффициентов прямых затрат сырья. Тогда полные затраты –го вида сырья, необходимые для производства валового продукта равны

.

Следовательно полные затраты всех видов сырья, необходимого на выполнение производственного задания, есть вектор

.

Определим затраты сырья в пересчете на 1 единицу конечной продукции 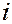–й отрасли. С учетом соотношения 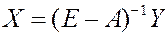получаем

.

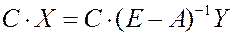Таким образом, матрица есть матрица коэффициентов полных затрат сырья.

Если известен вектор цен на одну единицу сырья каждого вида, ,

то полные затраты на производство конечного продукта равны ,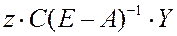

а себестоимость производства одной единицы продукции 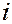-й отрасли равна

,

где 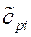- элемент матрицы , стоящий в 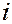-й строке, 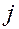-м столбце.

Определение себестоимости продукции.

Пусть в условиях предыдущей задачи для изготовления продукции каждого из трех цехов требуется 2 вида сырья (сырье а и сырье б), а также топливо и трудозатраты. Совокупные затраты этих 4 видов сырья раздельно по цехам приведены в таблице.

	Затраты по цехам	Стоимость 1 единицы сырья (руб)
I	II	III
Сырье а
Сырье б
Топливо
Труд

Требуется: определить коэффициенты затрат сырья в пересчете на 1 единицу конечной продукции и себестоимость 1 единицы конечной продукции, а также долю каждого сырья в себестоимости 1 единицы конечной продукции каждого вида.

Решение. Прежде всего, определим матрицу коэффициентов сырьевых затрат в пересчете на 1 единицу валовой продукции. Из таблицы видно, что на 1273.39 единиц валового продукта первого цеха пошло 1000, 500, 3000 и 1000 единиц сырья соответственно. Следовательно, удельные затраты на производство 1 единицы продукции первого цеха равны

.

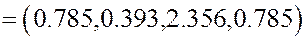Для второго цеха имеем

.

Для третьего цеха имеем

.

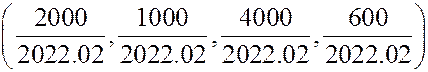
Матрица коэффициентов прямых затрат сырья имеет вид

.

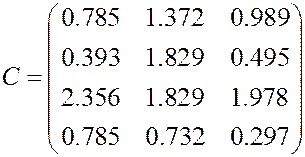Найдем коэффициенты полных затрат сырья (то есть пересчитаем затраты сырья на 1 единицу конечной продукции). Получаем

.

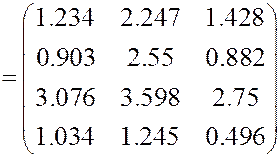Найдем себестоимость 1 единицы конечной продукции 1 цеха. Получаем:

рублей.

При этом доля сырья а в себестоимости составит

,

сырья б

,

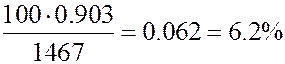топлива

,

и, наконец, доля труда составит

.

Для второго цеха получаем

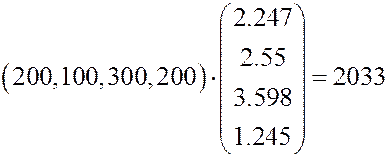рублей.

Для третьего цеха

.

Задача на дом.

Рассматривается трехотраслевая балансовая модель

Отрасли	Коэффициенты прямых затрат aij	Конечный продукт yi
I	II	III
I
II
III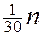

Определить: 1) коэффициенты полных затрат; 2) валовой выпуск; 3) производственную программу отраслей; 4) коэффициенты косвенных затрат.

Известны совокупные затраты 4 видов сырья раздельно по отраслям.

	Затраты по цехам	Стоимость 1 единицы сырья (руб)
I	II	III
Сырье а	1000	1500		200
Сырье б	500	2000		100
Топливо	3000	2000		300
Труд	1000	800	600	200

Требуется: определить коэффициенты затрат сырья в пересчете на 1 единицу конечной продукции и себестоимость 1 единицы конечной продукции, а также долю каждого сырья в себестоимости 1 единицы конечной продукции каждого вида.

Дата добавления: 2014-01-20