Теорема существования и единственности решения задачи Коши

Пусть имеем нормальную систему дифференциальных уравнений (3) и пусть функции 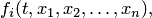, определены в некоторой n+1-мерной области 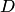изменения переменных . Если существует окрестность 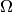точки 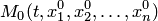, в которой функции а) непрерывны, 6) имеют ограниченные частные производные по переменным 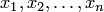, то найдется интервал 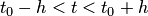изменения , в котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям (4).

Система 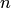дифференцируемых функций

(5)

независимой переменной и 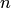произвольных постоянных 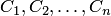называется общим решением нормальной системы (3), если: 1) при любых допустимых значениях 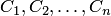система функций (5) обращает уравнения (3) в тождества, 2) в области, где выполняются условия теоремы Коши, функции (5) решают любую задачу Коши.

Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.

Введением новых функций

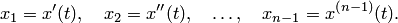
это уравнение заменяется нормальной системой 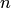уравнений

Можно утверждать и обратное, что, вообще говоря, нормальная система 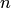уравнений первого порядка эквивалентна одному уравнению порядка 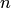. На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения.
Проиллюстрируем этот метод на примере системы двух уравнений:

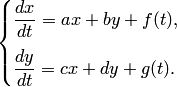
(1)

Здесь — постоянные коэффициенты, а 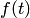и — заданные функци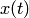и; и — искомые функции. Из первого уравнения системы (1) находим

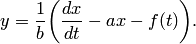
(2)

Подставляя во второе уравнение системы вместо у правую часть (2), а вместо производную от правой части (2), получаем уравнение at второго порядка относительно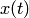

где 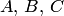— постоянные. Отсюда находим 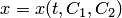. Подставив найденное выражение для 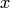и в (2), найдем .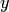

Нормальная линейная система дифференциальных уравнений с постоянными коэффициентами n-го порядка записывается в виде

где x ₁(t), x ₂(t),..., x_n (t) − неизвестные функции переменной t, которая часто имеет смысл времени, a_ij − заданные постоянные коэффициенты, которые могут быть как действительными, так и комплексными, f_i (t) − заданные (в общем случае комплексные) функции переменной t.

Будем считать, что все указанные функции являются непрерывными на некотором интервале [ a, b ]действительной числовой оси t.

Полагая

систему дифференциальных уравнений можно переписать в матричной форме:

Если вектор f (t) тождественно равен нулю: 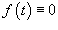, то система называется однородной:

Однородные системы уравнений с постоянными коэффициентами можно решать различными способами. Чаще всего используются следующие методы решений:

· метод исключения (метод сведения системы n уравнений к одному уравнению n -го порядка);

· метод интегрируемых комбинаций;

· метод собственных значений и собственных векторов (включая метод неопределенных коэффициентов или использование жордановой формы в случае кратных корней характеристического уравнения);

· метод матричной экспоненты.

Ниже на данной странице мы обсудим детально метод исключения. Другие способы решения систем уравнений рассматриваются отдельно на соответствующих страницах.

Дата добавления: 2014-01-20