КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Опр. 1.3.6. Полной механической энергией тела называется сумма кинетической и потенциальной энергий
|
|
|
|
Закон сохранения и превращения энергии: при любых процессах в замкнутых механических системах, где действуют только консервативные силы, полная энергия системы не изменяется 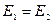 .
.
Закон сохранения энергии можно сформулировать не только для замкнутых, но и для открытых систем, где действуют внешние силы. При этом работа внешних сил сводится к изменению энергии системы  .
.
Если в системе действуют неконсервативные силы, например, силы трения, то полная механическая энергия системы может изменяться, превращаясь в другие виды (тепловую, химическую и т.д.). Рассматривая неконсервативные силы как внешние, можно записать 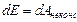 , т.е. изменение энергии системы равно работе неконсервативных сил.
, т.е. изменение энергии системы равно работе неконсервативных сил.
В более широком смысле, если рассматривать все возможные виды энергии, полная энергия замкнутой системы всегда сохраняется. Можно сказать, что энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии.
Рассмотрим применение закона к расчету
1) скорости поступательного движения тел после абсолютно неупругого (после удара тела движутся с одной и той же скоростью) прямого центрального (центры масс соударяющихся тел лежат на линии удара) удара. Пусть мы имеем два тела с массами  и
и 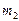 , движущимися навстречу друг другу со скоростями
, движущимися навстречу друг другу со скоростями  и
и  . По закону сохранения импульса
. По закону сохранения импульса 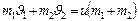 и скорость тел после удара
и скорость тел после удара 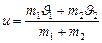 .
.
В этом случае кинетическая энергия системы частично преобразуется в ее внутреннюю энергию.
2) скорость поступательного движения тел после абсолютно упругого (механическая энергия соударяющихся тел не преобразуется в другие виды энергии) прямого центрального удара. Пусть мы имеем два тела с массами  и
и 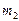 , движущимися навстречу друг другу со скоростями
, движущимися навстречу друг другу со скоростями и
и  . По закону сохранения импульса
. По закону сохранения импульса  , по закону сохранения механической энергии
, по закону сохранения механической энергии 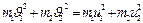 , тогда совместное решение уравнений дает скорости тел после удара
, тогда совместное решение уравнений дает скорости тел после удара  и
и 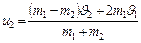 .
.
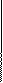 Пример 1.3.2.
Пример 1.3.2.
|
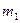 , движущийся горизонтально с некоторой скоростью, столкнулся с неподвижным шаром массы
, движущийся горизонтально с некоторой скоростью, столкнулся с неподвижным шаром массы 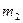 . Шары абсолютно упругие, удар прямой. Какую долю кинетической энергии первый шар передал второму?
. Шары абсолютно упругие, удар прямой. Какую долю кинетической энергии первый шар передал второму?
Решение:
 При ударе абсолютно упругих шаров одновременно выполняются:
При ударе абсолютно упругих шаров одновременно выполняются:
1) закон сохранения импульса (система шаров замкнута) 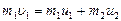 ;
;
2) закон сохранения энергии 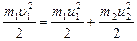 (т.к. силы консервативные).
(т.к. силы консервативные).
Решая совместно данные уравнения, получим  . Доля энергии, переданной первым шаром второму:
. Доля энергии, переданной первым шаром второму:  .
.
Т.о. движение твердого тела определяется приложенными к нему внешними силами.
При поступательном движении все точки твердого тела двигаются с одинаковыми скоростями и ускорениями. Если мысленно разбить твердое тело на элементы с массами 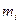 , то на каждый из них действует как внешняя сила
, то на каждый из них действует как внешняя сила 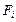 , так и внутренняя
, так и внутренняя  (со стороны других элементов), тогда по II закону Ньютона:
(со стороны других элементов), тогда по II закону Ньютона: 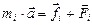 . По III закону Ньютона сумма всех внутренних сил равна нулю, поэтому суммируя полученное выражение по всем элементам получим:
. По III закону Ньютона сумма всех внутренних сил равна нулю, поэтому суммируя полученное выражение по всем элементам получим:  или
или 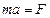 , где
, где  масса всего тела,
масса всего тела, 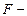 равнодействующая внешних сил, приложенных к системе.
равнодействующая внешних сил, приложенных к системе.
Рассмотрение поступательного движения твердого тела можно заменить рассмотрением движения одной материальной точки с массой, равной массе тела (обычно в качестве такой точки выбирают центр масс), и находящейся под действием силы, равной главному вектору внешних сил.
Вращательное движение рассмотрим в следующей главе.
§4. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 460; Нарушение авторских прав?; Мы поможем в написании вашей работы!