Гармонические колебания

Опр. 2.2.1. Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Простейший тип колебаний.

Уравнение гармонических колебани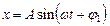й или ,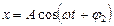

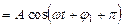где 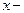смещение колеблющейся точки от положения равновесия, 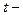время,

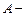амплитуда колебаний, равная максимальному абсолютному значению ,

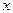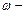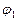круговая или циклическая частота – число полных колебаний, которые совершаются за единиц времени,

и 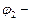начальные фазы колебани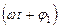й,

и 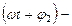фазы колебаний в момент времени 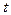. Вообще, фазой называют аргумент синуса или косинуса.

Установим связь между периодом и круговой частотой гармонических колебаний. Имеем .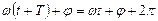

Отсюда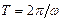

Между линейной частотой колебаний 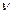и круговой частотой 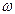существует связь: .

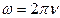Единица круговой частоты.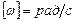

Скорость точки, совершающей гармонические колебания: 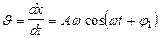или

Ускорение при гармоническом колебании:

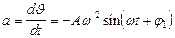или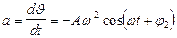

Т.к. 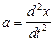, то дифференциальное уравнение гармонических колебаний: ,

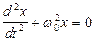где 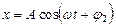является решением данного дифференциального уравнения, у которого величины 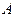и принимают любые значения. Для определения этих величин необходимо задать дополнительные условия.

Отметим, что уравнение 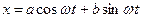описывает гармонические колебания. Применим метод дополнительного угла и получим 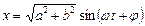, где , .

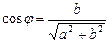Гармонические колебания играют важную роль, т.к. многие периодические колебания можно представить в виде суммы гармонических колебаний. Непериодические колебания называют квазипериодическими, если их в первом приближении или в небольших областях можно рассматривать как периодические.

Дата добавления: 2014-01-11