Теорема Гурвица

Критерий Рауса – Гурвица

УСТОЙЧИВОСТИ

АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ

В тех случаях, когда цепь описывается дифференциальным уравнением высокого порядка, исследование корней характеристического уравнения является сложной задачей. Оказывается устойчивость системы можно определить, не решая уравнения. Для этого служат критерии устойчивости.

Критерий Рауса – Гурвица относится к алгебраическим.

Для того чтобы действительные части всех корней характеристического уравнения с действительными коэффициентами и b₀ > 0 были отрицательными, необходимо и достаточно, чтобы были положительными все определители Δ₁, Δ₂,…, Δ_n, составленные из коэффициентов b₀, b₁,…, b_n по следующей схеме:

Δ₁ = b₁; Δ₂ =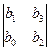; Δ₃ =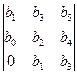; Δ₄=;Δ₅ =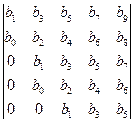; и т.д.

Пример для характеристического уравнения 5-го порядка:

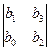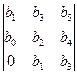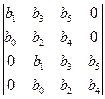Δ₁ = b₁; Δ₂ =; Δ₃ =; Δ₄=;Δ₅ =;

Отсюда следует, что

Δ_n = b_n * Δ_n-1.

Для определения числа корней в правой полуплоскости (неустойчивых) используется следующее положение:

Строится ряд

b₀, Δ₁, Δ₂/Δ₁,…, Δ_n-1,Δ_n-2, Δ_n/Δ_n-1.

Дата добавления: 2014-01-11