Методы изучения статистической связи

В процессе изучения связи надо учитывать, что мы используем математический аппарат, но всегда надо иметь теоретические обоснования той связи, которую пытаются показать.

Наиболее простой способ иллюстрации зависимости между двумя величинами — построение таблиц, показывающих, как при изменении одной величины меняется другая.

Пример 4.

Производство молока в год. тыс. тонн.	Выработка продукции на 1 работающего, тыс. руб.
до 31	34,2
31 — 50	37,3
51 и выше	42,7

Таблица показывает лишь согласованность в изменении двух величин, наличие связи. Но она не определяет, ни тесноту, ни форму этой связи.

Один из простых показателей тесноты корреляционной зависимости — показатель корреляции рангов. Разберем порядок вычисления этого показателя на примере.

Изучается товарооборот и суммы издержек обращения по ряду магазинов (в тыс. руб.). Данные представлены таблицей 1.

Таблица 4.8

№ магазина	Товарооборот	Издержки обращения

Из таблицы видно, что с ростом товарооборота растут и издержки обращения. График еще раз это подтверждает.

Но в ряде случаев увеличение товарооборота ведет и к уменьшению издержек обращения, поскольку, помимо двух названных величин, в реальном процессе торговли участвуют и другие факторы, которые в рассмотрение не включены и носят случайный характер. Рассмотрим критерий тесноты связи, названный показателем корреляции рангов. От величин абсолютных перейдем к рангам по такому правилу: самое меньшее значение — ранг 1, затем 2 и т.д. Если встречаются одинаковые значения, то каждое из них заменяется средним. Итак:

Товарооборот	Издержки
	7,5
	7,5

Построим разности между рангами и возведем их в квадрат.

1. Если ранги совпадают, то ясно, что сумма их квадратов равна 0.

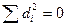
Связь полная, прямая.

2. Ранги образуют обратную последовательность

1 10

2 9 В этом случае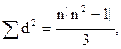

3 8

Связь полная, обратная.

3. Среднее значение из двух крайних означает полное отсутствие связи:

4. Показатель корреляции рангов:

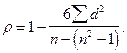
Показатель показывает, как отличается полученная при наблюдении сумма квадратов разностей между рангами от случая отсутствия связи.

Проанализируем показатель корреляции рангов.

1. Связь полная и прямая, 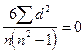и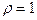

2. Связь полная и обратная, и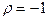

3. Все остальные значения лежат между -1 и +1.

Построим показатель корреляции рангов для нашего примера:

Товарооборот (ранг)	Издержки (ранг)
		-3
		-2
	7,5	-0,5	0,25
	7,5	0,5	0,25

Полученный показатель свидетельствует о достаточно тесной связи между товарооборотом и издержками.

Для определения тесноты корреляционной связи применяется коэффициент корреляции.

Коэффициент корреляции изменяется от -1 до +1 и показывает тесноту и направление корреляционной связи:

-Если отклонения 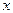по и по 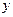от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то 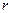=+1.

-Если полная обратная связь, то 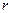=-1.

-Если связь отсутствует, то 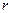=0.

Наиболее удобной формулой для расчета коэффициента корреляции является:

(1)

Коэффициент корреляции можно рассчитать и по другой формуле:

(2), где

и

Дата добавления: 2014-01-20