Определение LL(k)-грамматики

Логическим продолжением идеи, положенной в основу метода рекурсивного спуска, является предложение использовать для выбора одной из множества альтернатив не один, а несколько символов входной цепочки. Однако напрямую переложить алгоритм выбора альтернативы для одного символа на такой же алгоритм для цепочки символов не удастся — два соседних символа в цепочке на самом деле могут быть выведены с использованием различных правил грамматики, по­этому неверным будет напрямую искать их в одном правиле. Тем не менее, суще­ствует класс грамматик, основанный именно на этом принципе — выборе одной альтернативы из множества возможных на основе нескольких очередных симво­лов в цепочке. Это так называемые LL(k)-грамматики. Правда, алгоритм работы распознавателя для них не так очевидно прост, как рассмотренный выше алго­ритм рекурсивного спуска.

Грамматика обладает свойством LL(k), k > 0, если на каждом шаге вывода для однозначного выбора очередной альтернативы МП-автомату достаточно знать символ на верхушке стека и рассмотреть первые k символов от текущего поло­жения считывающей головки во входной цепочке символов.

Грамматика называется LL(k) -грамматикой, если она обладает свойством LL(k) для некоторого k > 0. (Требование k > 0, безусловно, является разумным — для принятия решения о выборе той или иной альтернативы МП-автомату надо рассмотреть хотя бы один символ входной цепочки. Если представить себе LL-грамматику с k = 0, то в такой грамматике вывод со­всем не будет зависеть от входной цепочки. В принципе такая грамматика возможна, но в ней будет всего одна-единственная цепочка вывода. Поэтому практическое применение языка, заданного такого рода грамматикой, представляется весьма сомнительным.)

Название «LL(k)» несет определенный смысл. Первая литера «L» происходит от слова «left» и означает, что входная цепочка символов читается в направлении слева направо. Вторая литера «L» также происходит от слова «left» и означает, что при работе распознавателя используется левосторонний вывод. Вместо «k» в названии класса грамматики стоит некоторое число, которое показывает, сколь­ко символов надо рассмотреть, чтобы однозначно выбрать одну из множества аль­тернатив. Так, существуют LL(1)-грамматики, LL(2)-грамматики и другие классы.

В совокупности все LL(k)-грамматики для всех k>0 образуют класс LL-грамматик.

На рис. 12.1 схематично показано частичное дерево вывода для некоторой LL(k)-грамматики. В нем w обозначает уже разобранную часть входной цепочки a, ко­торая построена на основе левой части дерева у. Правая часть дерева х — это еще не разобранная часть, а А — текущий нетерминальный символ на верхушке стека МП-автомата. Цепочка х представляет собой незавершенную часть цепочки вы­вода, содержащую как терминальные, так и нетерминальные символы. После за­вершения вывода символ А раскрывается в часть входной цепочки u, а правая часть дерева х преобразуется в часть входной цепочки t. Свойство LL(k) предпо­лагает, что однозначный выбор альтернативы для символа А может быть сделан на основе k первых символов цепочки ut, являющейся частью входной цепоч­ки a.

Алгоритм разбора входных цепочек для LL(k)-грамматики носит название «k-предсказывающего алгоритма». Принципы его выполнения во многом соответст­вуют функционированию МП-автомата с той разницей, что на каждом шаге работы этот алгоритм может просматривать k символов вперед от текущего поло­жения считывающей головки автомата.

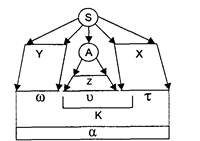
Рис. 12.1. Схема построения дерева вывода для LL(k)-грамматики

Для LL(k)-грамматик известны следующие полезные свойства:

· всякая LL(k)-грамматика для любого k>0 является однозначной;

· существует алгоритм, позволяющий проверить, является ли заданная грамма­тика LL(k)-грамматикой для строго определенного числа k.

Кроме того, известно, что все грамматики, допускающие разбор по методу рекур­сивного спуска, являются подклассом LL(1) -грамматик. То есть любая грамма­тика, допускающая разбор по методу рекурсивного спуска, является LL(1)-грам­матикой (но не наоборот!).

Есть, однако, неразрешимые проблемы для произвольных КС-грамматик:

· не существует алгоритма, который бы мог проверить, является ли заданная КС-грамматика LL(k)-грамматикой для некоторого произвольного числа k;

· не существует алгоритма, который бы мог преобразовать произвольную КС-грамматику к виду LL(k)-грамматики для некоторого k (или доказать, что преобразование невозможно).

Это несколько ограничивает применимость LL(k)-грамматик, поскольку не все­гда для произвольной КС-грамматики можно очевидно найти число k, для кото­рого она является LL(k)-грамматикой, или узнать, существует ли вообще для нее такое число k.

Для LL(k)-грамматики при k>l совсем не обязательно, чтобы все правые части правил грамматики для каждого нетерминального символа начинались с k различ­ных терминальных символов. Принципы распознавания предложений входного языка такой грамматики накладывают менее жесткие ограничения на правила грамматики, поскольку k соседних символов, по которым однозначно выбирает­ся очередная альтернатива, могут встречаться и в нескольких правилах грамма­тики (эти условия рассмотрены ниже). Грамматики, у которых все правые части правил для всех нетерминальных символов начинаются с k различных терми­нальных символов, носят название «сильно LL(k)-грамматик». Метод построе­ния распознавателей для них достаточно прост, алгоритм разбора очевиден, но, к сожалению, такие грамматики встречаются крайне редко.

Для LL(1)-грамматики, очевидно, для каждого нетерминального символа не мо­жет быть двух правил, начинающихся с одного и того же терминального симво­ла. Однако это менее жесткое условие, чем то, которое накладывает распознава­тель по методу рекурсивного спуска, поскольку в принципе LL(1)-грамматика допускает в правой части правил цепочки, начинающиеся с нетерминальных символов, а также l-правила. LL(1) -грамматики позволяют построить достаточ­но простой и эффективный распознаватель, поэтому они рассматриваются далее отдельно в соответствующем разделе.

Поскольку все LL(k) -грамматики используют левосторонний нисходящий рас­познаватель, основанный на алгоритме с подбором альтернатив, очевидно, что они не могут допускать левую рекурсию. Поэтому никакая леворекурсивная грам­матика не может быть LL-грамматикой. Следовательно, первым делом при по­пытке преобразовать грамматику к виду LL-грамматики необходимо устранить в ней левую рекурсию (соответствующий алгоритм был рассмотрен выше).

Класс LL-грамматик широк, но все же он недостаточен для того, чтобы покрыть все возможные синтаксические конструкции в языках программирования (к ним относим все детерминированные КС-языки). Известно, что существуют детер­минированные КС-языки, которые не могут быть заданы LL(k)-грамматикой ни для каких k. Однако LL-грамматики удобны для использования, поскольку по­зволяют построить распознаватели с линейными характеристиками (линейной зависимостью требуемых для работы алгоритма распознавания вычислительных ресурсов от длины входной цепочки символов).

Дата добавления: 2014-01-20