Диаграммы состояния

Вещество при изменении давления и температуры может переходить из одного агрегатного состояния в другое. Эти переходы, совершающиеся при постоянной температуре, называют фазовыми переходами первого рода.

Число степеней свободы гетерогенной термодинамической системы, находящейся в состоянии фазового равновесия, определяется правилом фаз, сформулированным Дж. Гиббсом:

Число степеней свободы равновесной термодинамической системы С равно числу независимых компонентов системы К минус число фаз Ф плюс число внешних факторов, влияющих на равновесие.

Правило устанавливает возможное число фаз и условия, при кото­рых они могут существовать в конкретной системе, а именно: С = = К + В - Ф, где С — число степеней свободы, определяет число независимых переменных (температура, концентрация, давление), которое можно изменять, не нарушая равновесия в системе, т.е. не изменяя числа фаз Ф; К — число компонентов; В — число внешних переменных факторов.

Для металлических сплавов можно принять В = 1 (из числа вне­шних факторов учитывается только температура), или правило фаз С = К+ 1-Ф.

Для системы, на которую из внешних факторов влияют только температура и давление, можно записать:

С = К – Ф + 2

Системы принято классифицировать по числу компонентов (одно-, двухкомпонентные и т.д.), по числу фаз (одно-, двухфазные и т.д.) и числу степеней свободы (инвариантные, моно-, дивариантные и т.д.). Для систем с фазовыми переходами обычно рассматривают графическую зависимость состояния системы от внешних условий – т.н. диаграммы состояния.

Анализ диаграмм состояния позволяет определить число фаз в системе, границы их существования, характер взаимодействия компонентов. В основе анализа диаграмм состояния лежат два принципа: принцип непрерывности и принцип соответствия. Согласно принципу непрерывности, при непрерывном изменении параметров состояния все свойства отдельных фаз изменяются также непрерывно; свойства системы в целом изменяются непрерывно до тех пор, пока не изменится число или природа фаз в системе, что приводит к скачкообразному изменению свойств системы. Согласно принципу соответствия, на диаграмме состояния системы каждой фазе соответствует часть плоскости – поле фазы. Линии пересечения плоскостей отвечают равновесию между двумя фазами. Всякая точка на диаграмме состояния (т. н. фигуративная точка) отвечает некоторому состоянию системы с определенными значениями параметров состояния.

Рассмотрим и проанализируем диаграмму состояния воды (рис.1.4). Поскольку вода – единственное присутствующее в системе вещество, число независимых компонентов К = 1. В системе возможны три фазовых равновесия: между жидкостью и газом (линия ОА – зависимость давления насыщенного пара воды от температуры), твердым телом и газом (линия ОВ – зависимость давления насыщенного пара надо льдом от температуры), твердым телом и жидкостью (линия ОС – зависимость температуры плавления льда от давления). Три кривые имеют точку пересечения О, называемую тройной точкой воды; тройная точка отвечает равновесию между тремя фазами.

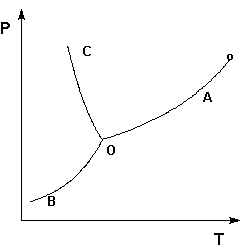
Рис. 1.4. Диаграмма состояния воды

В тройной точке система трехфазна и число степеней свободы равно нулю; три фазы могут находиться в равновесии лишь при строго определенных значениях температуры и давления (для воды тройная точка отвечает состоянию с Р = 6.1 кПа и Т = 273.16 К).

Кривая ОВ теоретически продолжается до абсолютного нуля, а кривая давления насыщенного пара над жидкостью ОА заканчивается в критической точке воды (T_кр = 607.46 К, Р_кр = 19.5 МПа); выше критической температуры газ и жидкость не могут существовать как отдельные фазы. Кривая ОС в верхней части (при высоких давлениях) изменяет свой наклон (появляются новые кристаллические фазы, плотность которых, в отличие от обычного льда, выше, чем у воды).

Внутри каждой из областей диаграммы (АОВ, ВОС, АОС) система однофазна; число степеней свободы системы равно двум (система дивариантна), т.е. можно одновременно изменять и температуру, и давление, не вызывая изменения числа фаз в системе:

С = 1 – 1 + 2 = 2

На каждой из линий число фаз в системе равно двум и, согласно правилу фаз, система моновариантна, т.е. для каждого значения температуры имеется только одно значение давления, при котором система двухфазна:

С = 1 – 2 + 2 = 1

Реальные диаграммы состояния подчас являются очень сложными [1], поэтому имеет смысл начать рассмотрение с отдельных типов диаграмм.

В материаловедении взаимодействие компонентов в сплаве, характер образующихся структур и свой­ства сплавов определяют экспериментальным путем. С этой целью для каждого конкретного сплава строят экспериментальные кри­вые охлаждения и нагрева сплавов в координатах температура — время.

На получаемых графиках в виде площадок проявляются крити­ческие точки, соответствующие критическим температурам, при которых происходят превращения в кристаллической решетке сплава. Соединяя получаемые критические температурные точки на диаграмме температура—состав, получают линии диаграммы состояния. Геометрическое место всех точек, которые определяют температуру начала кристаллизации, называют линией ликвидуса (L), а температуру конца кристаллизации — линией солидуса (S).

Таким образом, на базе изучения полученных микроструктур, определения типа и параметров кристаллической решетки, а так­же свойств сплавов и кривых охлаждения строится диаграмма со­стояния (диаграмма равновесия) любой изучаемой системы, ко­торая в удобной графической форме отражает фазовое состояние сплавов этой системы в зависимости от температуры и концент­рации компонентов. По диаграмме состояния можно установить превращения, которые претерпевает любой из сплавов системы при нагреве (охлаждении), определить температуры плавления или затвердевания сплава, выбрать рациональный режим термичес­кой обработки, прогнозировать поведение сплава в заданном ин­тервале температур.

Дата добавления: 2014-01-20