Ранг матрицы. Теорема о базисном миноре. Необходимое и достаточное условия равенства определителя нулю

Лекция 5

Понятие о полигенном наследовании

Карты хромосом человека

Открытия Моргана создали основу для определения мест расположения генов и оценки расстояния между ними. Расстояние между генами измеряется частотой кроссинговера. Т.есть отношением кол-ва особей, которые унаследовали только один ген, к числу тех, у кого были представлены совместно 2 гена, выраженное в %, ед. такого расстояния является 1% кроссинговера – 1сантиморганида.

Расстояние между генами в 1% кроссинговера показывает, что они обычно передаются потомкам совместно (сцеплено).

Если 50% - гены наследуются независимо друг от друга.

Возможность оценки расстояния между генами стала основой для построения генетических карт.

Г.К хромосомы – отрезок прямой, на котором указывается порядок расположения генов относительно друг друга и расстояние между ними в сантиморганидах.

Созданы генетические паспорта. Используются на практике экспертные системы. Проведение подобных работ влечет за собой очень много вопросов не только технических, но и нравственных, социальных, экономических.

Исследование генома открывает путь молекулярной медицине для Дз, лечения и профилактики наследственных заболеваний

Всех людей можно условно разделить по фенотипическим характеристикам.

Если признаки определяются совместным действием нескольких пар неаллельных генов, каждый из которых вносит свой вклад – такое наследование - полигенное

Если влияние каждого гена из такой группы примерно одинаковое - это аддиктивное действие.

ПГН – одновременное наследование признаков, которые кодируются несколькими генами, или взаимодействием генов.

Главная основа – индивидуальность каждого человека, обусловленная уникальностью его генома. Профилактическая направленность всех программ, позволяющая предупредить направленность заболевания до его начала!

Важнейшей особенностью полигенных признаков является зависимость их проявления от действия факторов внешней среды, которые могут значительно изменять из фенотипические характеристики.

Рассмотрим матрицу , , :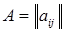

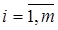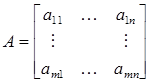
Определение 1. Если матрица А – нулевая, то ранг матрицы А равен 0. Если же матрица А – ненулевая, то рангом матрицы А называется минимальный порядок минора, не равного 0.

Обозначение: r(A), Rang A

Примеры: 1. r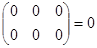

2. r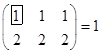, т.к. существует ненулевой минор порядка 1 (например, расположенный в верхнем левом углу), а все миноры второго порядка равны 0.

Определение 2. Ненулевой минор порядка, равного рангу матрицы, называется базисным минором. Строки и столбцы матрицы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами.

Замечание. Базисных миноров может быть несколько. Фиксируя новый минор в качестве базисного, мы тем самым получаем новые базисные строки и столбцы.

Пример. Из определения ранга матрицы следует, что вычисление ранга матрицы следует вести постепенно, повышая порядок вычисляемых миноров. Например, найдем ранг матрицы А:

; ; ; ;

; ; .

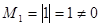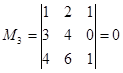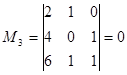Видим, что существует минор 2-ого порядка, не равный 0, а все миноры 3-го порядка равны 0. Следовательно, Rang A=2.

Теорема. (о базисном миноре) Базисные строки (столбцы) образуют линейно независимую систему. Остальные строки (столбцы) являются линейными комбинациями базисных строк (столбцов).

Доказательство. Пусть Rang A=r. Докажем теорему для столбцов, для строк все доказательство проводится аналогично.

Пусть для определенности базисный минор (ненулевой минор порядка r) расположен в верхнем левом углу матрицы А. Если это не так, переместим базисный минор в верхний левый угол, переставляя строки и столбцы матрицы (очевидно, что ранг матрицы А при таких преобразований матрицы не изменится).

Пусть базисный минор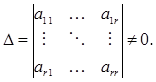

Все миноры порядка выше r равны 0. Предположим, что базисные столбцы образуют линейно зависимую систему. В этом случае базисный минор ∆ состоял бы из столбцов, один из которых является линейной комбинацией остальных столбцов этого минора. Следовательно, в этом случае, в силу свойств определителей, получили бы, что 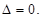Полученное противоречие доказывает, что базисные столбцы не могут образовывать линейно зависимую систему.

Докажем, что небазисные столбцы есть линейная комбинация базисных. Докажем это для l го столбца (). Рассмотрим вспомогательные определители порядка (r+1) вида:

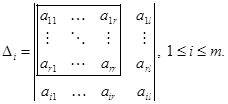
Имеем:

1) для 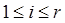, т.к. определитель 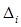содержит две одинаковых строки; 2) для 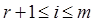, так как в этом случае 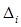есть минор порядка (r+1) го порядка матрицы А, а все миноры порядка, большего, чем r, должны быть равны 0 (т.к. Rang A=r). Отсюда: 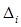=0 для 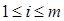. Выпишем разложение определителя 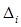по i той строке:

, .

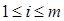Здесь алгебраические дополнения к элементам (r+1) й строки определителя 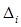, они не зависят от номера i. Из последних равенств выражаем элементы l го столбца:

m равенств.

Следовательно,

Следовательно, l й столбец (l > r) есть линейная комбинация базисных столбцов , взятых с коэффициентами

▲

Замечание. В доказательстве теоремы о базисном миноре используются только миноры, окаймляющие (т.е. содержащие в себе) базисный минор. Отсюда получаем метод окаймляющих миноров вычисления ранга матрицы.

Пример. Вычислим ранг матрицы А, используя метод окаймляющих миноров:

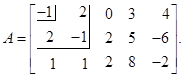
Фиксируем минор 1-го порядка, не равный 0: 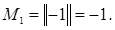Окаймляем его: находим минор 2го порядка, не равный 0, окаймляющий минор :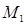

Выпишем и вычислим миноры 3го порядка, окаймляющие ненулевой минор :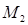

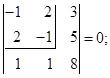
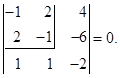
Так как все окаймляющие миноры 3го порядка равны 0, делаем вывод, что Rang A=2.

Дата добавления: 2014-01-20