Геометрических параметров изделий

Научно-методические основы обеспечения точности

Фактический размер строительных изделий, полученный в результате

измерения соответствующим инструментом, отличается от конструктивного,

предусмотренного рабочими чертежами, и называется действительным.

Отклонения действительных размеров от номинальных (конструктивных) не

должны выходить за нормируемые пределы.

Для назначения и оценки точности геометрического параметра,

например линейного размера строительного изделия х, представляющего

собой случайную величину, используют комплекс характеристик,

взаимосвязь между которыми представлена на рисунке 5.

Рисунок 5 - Характеристики точности геометрического параметра

(размера х)

Точность геометрического параметра (размера) характеризуют

значением действительного отклонения δхi:

δхi = хi – хном, (1)

где хi – действительные значения размера;

хном – номинальное значение, называемое базисным (указывают в

проекте).

Характеристиками точности размеров в стандартах являются: хmin и

хmax – минимальный и максимальный предельные размеры, между которыми

должны находиться действительные значения с определенной вероятностью;

δxinf, δxsup – нижнее и верхнее предельные отклонения от номинального

размера хnom, представляющие собой алгебраическую разность между

предельными и номинальными размерами; ∆ х – допуск размера – абсолютное

значение разности предельных размеров. Вся совокупность значений

геометрического параметра (размера), ограниченная его предельными

размерами, образует поле допуска; δxc – отклонение середины поля допуска

от номинального размера хnom; δ x =

Дх

- предельное отклонение размера х от

середины поля допуска хc, равное половине поля допуска.

Перечисленные характеристики связаны между собой. Предельные

размеры определяют по формулам:

хmin = хnom + δxinf = хc – δx; (2)

хmax = хnom + δxsup = хc + δx. (3)

Значения δxinf и δxsaр подставляют в формулы (2) и (3) со своими

знаками.

Допуск размера

∆х = 2δx = хmax - хmin = δxsup - δxinf. (4)

Отклонения середины поля допуска

дхс = хс − х nom =

x max − x min

− x nom =

дxsup + дxinf

. (5)

Действительные значения хi геометрического параметра х образуют

некоторую совокупность, для оценки которой используют статистические

характеристики точности: среднее значение геометрического параметра mx и

среднее квадратическое отклонение σx. В случае распределения значений

геометрического параметра по нормальному закону статистическими

оценками характеристик mx и σx являются выборочное среднее хm и

выборочное среднее квадратическое отклонение Sx.

∑ x i

х m =

1 n

n i=1

(6)

Sx = 

  2 

∑=i 1 (x i − x m) 

 1

 n − 1

n



1

, (7)

где n – объем выборки.

Систематическое отклонение δmx размера представляет собой

разность между средним и номинальным его значением

δmx = mx - хnom. (8)

При нормальном распределении оценкой δmx является выборочное

среднее отклонение δxm – среднее отклонение в выборках

δxm = xm - хnom. (9)

Предельные размеры хmin и хmax устанавливают по формулам:

хmin = mx - tminσx, (10)

хmax = mx + tmaxσx, (11)

где tmin, tmax – значения стандартизированной случайной величины,

зависящие от вероятности появления значений ниже xmin и выше xmax, а также

от типа статистического распределения параметра x.

Вероятность появления x ниже xmin и выше xmax принимают

одинаковой, но не более 0,05.

При нормальном распределении значений геометрического параметра

и одинаковой вероятности появления x ниже xmin и выше xmax принимают tmin

= tmax = 1. Тогда:

хс = mx, (12)

где хс – середина поля допуска.

хmin = хnom + δxс – δx, (13)

хmах = хnom + δxс + δx. (14)

Если при этом mx практически не отличается от хnom, то применимы

следующие зависимости:

δxс = δmx = 0, (15)

δxinf = δxsup = δx, (16)

хmin = хnom – δx, (17)

хmax = хnom + δx. (18)

Интервал номинального размера L	Значения допусков для класса точности
До 20 Свыше 20 до 60 Свыше 60 до 120 Свыше 120 до 250	0,24 0,3 0,4 0,5	0,4 0,5 0,6 0,8	0,6 0,8 1,0 1,2	1,0 1,2 1,6 2,0	1,6 2,0 2,4 3,0	2,4 3,0 4, 5,0	4,0 5,0 6,0 8,0	6,0 8,0 10,0 12,0	10,0 12,0 16, 20,0
Значения К	0,10	0,16	0,25	0,40	0,60	1,0	1,6	2,5	4,0

При оценке точности следует пользоваться предельными

отклонениями относительно хnom. Как правило, (при δxс = 0) предельные

отклонения принимают равными по абсолютному значению половине

значения соответствующего функционального или технологического

допуска, использованного в расчете точности.

Функциональным называют допуск геометрического параметра,

устанавливающего точность собранной конструкции из условий обеспечения

предъявляемых к ней функциональных требований. К функциональным

допускам относят: допуск зазора между элементами, допуски соосности.

Конкретные значения функциональных допусков определяют по формуле

(19). Расчетная схема определения допусков приведена на рисунке 6.

Технологическим называют допуск геометрического параметра,

устанавливающий точность выполнения соответствующего

технологического процесса по изготовлению и установке строительных

элементов. Значения функциональных и технологических допусков, в мм или

угловых величинах, должны соответствовать числовому ряду: 1; 1,6; 2,4; 4; 6;

10 или 1; 1,2; 1,6; 2; 2,4; 3; 4; 5; 6; 8; 10. Каждое число ряда можно увеличить

или уменьшить умножением его на 10 m, где m – целое число (положительное

или отрицательное).

В таблице 2 представлены конкретные значения технологических

допусков некоторых линейных размеров строительных элементов.

Таблица 2 – Технологические допуски линейных размеров, мм

Технологические допуски и предельные отклонения геометрических

параметров назначают, как правило, различных классов точности в

зависимости от функциональных, конструктивных, технологических и

экономических требований. Под классом точности подразумевают

совокупность значений технологических допусков, зависящих от

номинальных значений геометрических параметров.

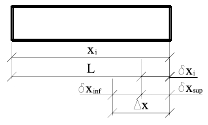
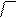
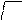
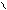
Рисунок 6 – Расчетная схема определения допусков

Значения технологических допусков ∆ х, мм, приведенные в таблице,

вычислены по формуле

∆х = iК, (19)

где i – единица допуска, мм;

К – коэффициент точности, устанавливающий число единиц

допуска для данного класса точности.

При изготовлении строительных изделий единицу допуска

определяют по формуле:

i = a i (0,8 + 0,001 L)(3 L + 25 + 0,013 L2), (20)

где L – номинальный размер, выражают в мм;

ai – множитель, принимают равным 1 при расчете допусков

линейных размеров прямолинейности, плоскостности, равенства диагоналей;

и равным 0,6 при расчете перпендикулярности поверхностей изделия.

Для кирпича керамического размером 250×120×65 мм, если принять

шестой класс точности, допуск по толщине будет составлять:

∆х = iК = i·1,0

i = a i (0,8 + 0,001 65)(3 65 + 25 + 0,01 3 65 2) = 3,74 мм

∆х = 3,74·1,0 = 3,74

а для ширины равной 120 мм:

i = a i (0,8 + 0,001 120)(3 120 + 25 + 0,01 3 120 2) = 4,45 мм

Дата добавления: 2014-01-20