
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделирование средств измерений
|
|
|
|
Построение и изучение СИ невозможно без математических моделей, адекватно описывающих те или иные их свойства и характеристики. В метрологии используется моделирование измерительных сигналов и моделирование средств измерений. Модель является представлением объекта в некоторой форме, отличной от формы его реального существования. Модель может быть похожей копией объекта, выполненной из другого материала, в другом масштабе, с отсутствием ряда деталей. Модель может, однако, отображать реальность более абстрактно - словесным описанием в свободной форме, описанием, формализованным по каким-то правилам, математическими соотношениями и т.д.
Первый этап - определение целей моделирования. Основные из них таковы:
1) модель нужна для того, чтобы понять как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание);
2) модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);
3) модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).
Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием (разделением по рангам). Чаще всего невозможно (да и не нужно) учитывать все факторы, которые могут повлиять на значения интересующих нас величин yj.
Для построения математических моделей (ММ) СИ необходимо знать, как устроены СИ и каким образом происходит преобразование измерительных сигналов, т.е. нужно знать структуру СИ. Для сложных СИ, каковыми являются большинство современных приборов, анализ их составных частей и ММ является далеко не простой задачей. Для ее оптимального решения, а также для упрощения анализа процессов, протекающих в СИ, введены понятия структурной схемы и измерительных цепи, канала и тракта.
|
|
|
Измерительная цепь — совокупность элементов СИ, образующих непрерывный путь прохождения измерительного сигнала от входа до выхода и обеспечивающих осуществление всех его преобразований.
Измерительный канал — это измерительная цепь, образованная последовательным соединением СИ и других технических устройств, предназначенная для измерения одной величины и имеющая нормированные метрологические характеристики.
Измерительный тракт — совокупность измерительных каналов, предназначенных для измерения определенной величины и имеющих одинаковые метрологические характеристики.
Структурная схема - условное обозначение измерительной цепи (канала или тракта) СИ с указанием преобразуемых величин. Эта схема определяет основные структурные блоки СИ, их назначение и взаимосвязи.
Структурные элементы могут быть классифицированы по ряду признаков. По типу выходного сигнала они разделяются на активные, генерирующие физические величины — носители энергии (например, аккумуляторы, усилители сигналов разного рода, источники света, излучения и др.), и пассивные, свойства которых зависят от состояния материи и выражаются физическими величинами, не являющимися носителями энергии (например, электрические сопротивления, емкости, индуктивности, оптические элементы — призмы, зеркала и др.).
По виду связи между входной и выходной величинами структурные блоки делятся на линейные и нелинейные. Линейными называются блоки, передаточные функции которых удовлетворяют условиям аддитивности f[X,(t) + X2(t)] = f[X,(t)] + f[X2(t)] и однородности f[CX(t)] = Cf[X(t)]. Параметры линейных блоков не зависят от параметров входного сигнала. Это наиболее простой и удобный для анализа тип блоков, поэтому для решения измерительной задачи по возможности следует выбирать линейные элементы. Примером линейного блока является идеальный усилитель.
|
|
|
Для нелинейных блоков связь между входным и выходным сигналами описывается функцией f, не удовлетворяющей приведенным выше условиям. Эти блоки делятся на квазилинейные и функциональные. Квазилинейные блоки характеризуются незначительной нелинейностью и считаются линейными при изменении входной и выходной величин в определенных диапазонах. Функциональным блокам присуща значительная нелинейность, которая учитывается построением соответствующей нелинейной математической модели.
В зависимости от динамических свойств структурные блоки делятся на статические и динамические. В статических блоках взаимосвязь между выходной и входной величинами не зависит от скорости изменения входного сигнала и его производных более высоких порядков. Если такую зависимость необходимо учитывать, то данный структурный блок следует считать динамическим. Различают динамические блоки первого, второго и высших порядков.
Структурные блоки также классифицируются по функции, выполняемой в СИ. По этому признаку они делятся на усилители различных видов, делители, дифференциаторы, интеграторы, коммутаторы, ключи, АЦП, ЦАП, фильтры и др.
3.5. Принципы обработки данных и расчет погрешности ИК
Принципы обработки данных и расчет погрешности ИК 77
Результат измерения. 77
Обработка результатов измерений 78
Идентификация формы распределения результатов измерений 82
Однократные измерения 84
Косвенные измерения 88
Совместные и совокупные измерения 97
Основы теории суммирования погрешностей 99
Суммирование систематических погрешностей 103
Суммирование случайных погрешностей. 106
Суммирование систематических и случайных погрешностей 109
Критерий ничтожно малой погрешности. 111
Классы точности средств измерений 115
Принципы обработки данных и расчет погрешности ИК
Однократные и многократные измерения, методика обработки и представления результатов. Косвенные измерения, методика обработки результатов косвенных измерений, процесс обработки результатов совокупных и совместных измерений. Равноточные и неравноточные измерения: особенности выполнения, оценка результата и погрешности. Основы теории суммирования погрешностей: суммирование систематических и случайных погрешностей средств измерений; критерий ничтожно малой погрешности.
|
|
|
Классы точности средств измерений. Методика расчета погрешности ИК по нормированным метрологическим характеристикам.
Результат измерения.
Понятие результата измерения.
Результат - значение ФВ, полученное путем ее измерения. Результат измерения представляется именованным или неименованным числом. Совместно с результатом измерений при необходимости приводят данные об условиях измерений.
При использовании термина "результат измерения" следует четко указать, к чему он относится: показанию СИ, исправленному или не исправленному результату, и проводилось ли усреднение результатов нескольких измерений. Следует отметить, что исправленным результатом измерений называется полученное с помощью СИ значение величины и уточненное путем введения в него необходимых поправок на действие предполагаемых систематических погрешностей.
Понятие точности измерения.
Точность измерения - характеристика качества измерения, отражающая близость к нулю погрешности его результата. Точность измерения является величиной качественной. Высокая точность измерения соответствует малым погрешностям и наоборот. Иногда точность количественно оценивают обратной величиной модуля относительной погрешности. Например, если погрешность составляет 0,001, то точность равна 1000. Однако количественная оценка точности широкого распространения не получила.
Представление результата измерения.
Согласно МИ 1317 – 86 различают четыре формы представления результата измерения:
х, Δ от Δн до Δв, р(Δ).
|
|
|
х, Δс от Δс.н. до Δс.в., р(Δс), σ(Δ0).
х, σ(Δс), рст(Δс), σ(Δ0), рст(Δ0).
х, закон распределения Δс, закон распределения Δ0.
Обработка результатов измерений
Прямые многократные измерения
Равноточные измерения
Прямые многократные измерения делятся на равно- и неравноточные. Теоретические основы и методика объединения результатов неравноточных измерений подробно рассмотрены в [3]. Равно точными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. При равноточных измерениях СКО результатов всех рядов измерений равны между собой.
Перед проведением обработки результатов измерений необходимо удостовериться в том, что данные из обрабатываемой выборки статистически подконтрольны, группируются вокруг одного и того же центра и имеют одинаковую дисперсию. Устойчивость изменений часто оценивают интуитивно на основе длительных наблюдений. Однако существуют математические методы решения поставленной задачи — так называемые методы проверки однородности [3]. Применительно к измерениям рассматривается однородность групп наблюдений, необходимые признаки которой состоят в оценке несмещенности средних арифметических и дисперсий относительно друг друга.
Проверка допустимости различия между оценками дисперсий нормально распределенных результатов измерений выполняется с помощью критерия Р.Фишера при наличии двух групп наблюдений и критерия М.Бартлетта, если групп больше.
Задача обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится ее истинное значение. Обработка должна проводится в соответствии с ГОСТ 8.207—76 "ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения".
Исходной информацией для обработки является ряд из n (n > 4) результатов измерений  , из которых исключены известные систематические погрешности, — выборка. Число n зависит как от требований к точности получаемого результата, так и от реальной возможности выполнять повторные измерения.
, из которых исключены известные систематические погрешности, — выборка. Число n зависит как от требований к точности получаемого результата, так и от реальной возможности выполнять повторные измерения.
Последовательность обработки результатов прямых многократных измерений состоит из ряда этапов.
Определение точечных оценок закона распределения результатов измерений. На этом этапе определяются:
• среднее арифметическое значение х измеряемой величины;
• СКО результата измерения Sx;
• СКО среднего арифметического значения  .
.
Грубые погрешности и промахи исключаются, после чего проводится повторный расчет оценок среднего арифметического значения и его СКО. В ряде случаев для более надежной идентификации закона распределения результатов измерений могут определяться другие точечные оценки: коэффициент асимметрии, эксцесс и контрэксцесс, энтропийный коэффициент.
Определение закона распределения результатов измерений или случайных погрешностей измерений. В последнем случае от выборки результатов измерений 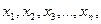 переходят к выборке отклонений от среднего арифметического
переходят к выборке отклонений от среднего арифметического 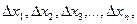 где
где 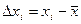 .
.
Первым шагом при идентификации закона распределения является построение по исправленным результатам измерений 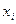 , где i=1, 2,..., n, вариационного ряда (упорядоченной выборки), а также
, где i=1, 2,..., n, вариационного ряда (упорядоченной выборки), а также 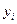 , где
, где 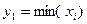 и
и  В вариационном ряду результаты измерений (или их отклонения от среднего арифметического) располагают в порядке возрастания. Далее этот ряд разбивается на оптимальное число т, как правило, одинаковых интервалов группирования длиной
В вариационном ряду результаты измерений (или их отклонения от среднего арифметического) располагают в порядке возрастания. Далее этот ряд разбивается на оптимальное число т, как правило, одинаковых интервалов группирования длиной 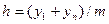 .
.
Задача определения оптимального числа m интервалов группирования рассматривалась в ряде работ, обзор которых дан в [4]. Оптимальным является такое число интервалов т, при котором возможное максимальное сглаживание случайных флуктуации данных сопровождается с минимальным искажением от сглаживания самой кривой искомого распределения. Для практического применения целесообразно использовать предложенные в [4] выражения 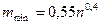 и
и 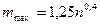 , которые получены для наиболее часто встречающихся на практике распределений с эксцессом, находящимся в пределах от 1,8 до 6, т.е. от равномерного до распределения Лапласа.
, которые получены для наиболее часто встречающихся на практике распределений с эксцессом, находящимся в пределах от 1,8 до 6, т.е. от равномерного до распределения Лапласа.
Искомое значение m должно находится в пределах от 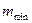 до
до 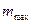 , быть нечетным, так как при четном m в островершинном или двухмодальном симметричном распределении в центре гистограммы оказываются два равных по высоте столбца и середина кривой распределения искусственно уплощается. В случае, если гистограмма распределения явно двухмодальная, число столбцов может быть увеличено в 1,5-2 раза, чтобы на каждый из двух максимумов приходилось примерно по m интервалов. Полученное значение длины интервала группирования h всегда округляют в большую сторону, иначе последняя точка окажется за пределами крайнего интервала.
, быть нечетным, так как при четном m в островершинном или двухмодальном симметричном распределении в центре гистограммы оказываются два равных по высоте столбца и середина кривой распределения искусственно уплощается. В случае, если гистограмма распределения явно двухмодальная, число столбцов может быть увеличено в 1,5-2 раза, чтобы на каждый из двух максимумов приходилось примерно по m интервалов. Полученное значение длины интервала группирования h всегда округляют в большую сторону, иначе последняя точка окажется за пределами крайнего интервала.
Далее определяют интервалы группирования экспериментальных данных в виде 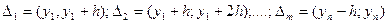 , и подсчитывают число попаданий
, и подсчитывают число попаданий 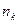 (частоты) результатов измерений в каждый интервал группирования. Сумма этих чисел должна равняться числу измерений. По полученным значениям рассчитывают вероятности попадания результатов измерений (частости) в каждый из интервалов группирования по формуле
(частоты) результатов измерений в каждый интервал группирования. Сумма этих чисел должна равняться числу измерений. По полученным значениям рассчитывают вероятности попадания результатов измерений (частости) в каждый из интервалов группирования по формуле 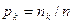 , где k=l, 2,..., m.
, где k=l, 2,..., m.
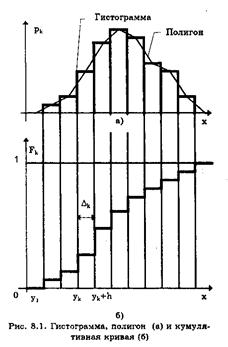
Проведенные расчеты позволяют построить гистограмму, полигон и кумулятивную кривую. Для построения гистограммы по оси результатов наблюдений х (рис. 8.1,а) откладываются интервалы 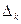 в порядке возрастания номеров и на каждом интервале строится прямоугольник высотой
в порядке возрастания номеров и на каждом интервале строится прямоугольник высотой 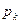 . Площадь, заключенная под графиком, пропорциональна числу наблюдений n. Иногда высоту прямоугольника откладывают равной эмпирической плотности вероятности
. Площадь, заключенная под графиком, пропорциональна числу наблюдений n. Иногда высоту прямоугольника откладывают равной эмпирической плотности вероятности 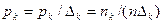 , которая является оценкой средней плотности в интервале
, которая является оценкой средней плотности в интервале 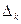 . В этом случае площадь под гистограммой* равна единицею При увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более приближается к гладкой кривой — графику плотности распределения вероятности» Следует отметить, что в ряде случаев производят расчетное симметрирование гистограммы.
. В этом случае площадь под гистограммой* равна единицею При увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более приближается к гладкой кривой — графику плотности распределения вероятности» Следует отметить, что в ряде случаев производят расчетное симметрирование гистограммы.
Полигон представляет собой ломаную кривую, соединяющую середины верхних оснований каждого столбца гистограммы (см. рис. 8.1,а). Он более наглядно, чем гистограмма, отражает форму кривой распределения. За пределами гистограммы справа и слева остаются пустые интервалы, в которых точки, соответствующие их серединам, лежат на оси абсцисс.
Эти точки при построении полигона соединяют между собой отрезками прямых линий. В результате совместно с осью х образуется замкнутая фигура, площадь которой в соответствии с правилом нормирования должна быть равна единице (или числу наблюдений при использовании частостей). Кумулятивная кривая — это график статистической функции распределения. Для ее построения по оси результатов наблюдений х (рис. 8.1,6) откладывают интервалы Ak в порядке возрастания номеров и на каждом интервале строят прямоугольник высотой 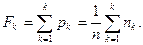

Значение 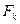 называется кумулятивной частостью, а сумма
называется кумулятивной частостью, а сумма 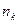 — кумулятивной частотой. По виду построения зависимостей может быть оценен закон распределения результатов измерений.
— кумулятивной частотой. По виду построения зависимостей может быть оценен закон распределения результатов измерений.
Оценка закона распределения по статистическим критериям. При числе наблюдений n>50 для идентификации закона распределения используется критерий Пирсона (хи-квадрат, см. 8.1.2) или критерий Мизеса—Смирнова (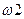 ). При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий (d-критерий), приведенный в ГОСТ 8.207-76. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.
). При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий (d-критерий), приведенный в ГОСТ 8.207-76. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.
Определение доверительных границ случайной погрешности. Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находят квантильный множитель zp при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности 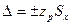 .
.
Определение границ неисключенной систематической погрешности 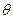 результата измерений. Под этими границами понимают найденные нестатистическими методами границы интервала, внутри которого находится неисключенная систематическая погрешность. Она образуется из ряда составляющих: как правило, погрешностей метода и средств измерений, а также субъективной погрешности. Границы неисключенной систематической погрешности принимаются равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составляющие пренебрежимо малы. Они суммируются по правилам, рассмотренным в разд. 9.2. Доверительная вероятность при определении границ
результата измерений. Под этими границами понимают найденные нестатистическими методами границы интервала, внутри которого находится неисключенная систематическая погрешность. Она образуется из ряда составляющих: как правило, погрешностей метода и средств измерений, а также субъективной погрешности. Границы неисключенной систематической погрешности принимаются равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составляющие пренебрежимо малы. Они суммируются по правилам, рассмотренным в разд. 9.2. Доверительная вероятность при определении границ 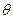 принимается равной доверительной вероятности, используемой при нахождении границ случайной погрешности.
принимается равной доверительной вероятности, используемой при нахождении границ случайной погрешности.
Определение доверительных границ погрешности результата измерения 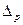 . Данная операция осуществляется путем суммирования СКО случайной составляющей
. Данная операция осуществляется путем суммирования СКО случайной составляющей 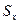 и границ неисключенной систематической составляющей
и границ неисключенной систематической составляющей 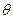 в зависимости от соотношения
в зависимости от соотношения 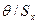 по правилам, изложенным в разд. 9.4.
по правилам, изложенным в разд. 9.4.
Запись результата измерения. Результат измерения записывается в виде 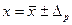 при доверительной вероятности
при доверительной вероятности 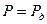 . При отсутствии данных о виде функции распределения составляющих погрешности результаты измерений представляют в виде
. При отсутствии данных о виде функции распределения составляющих погрешности результаты измерений представляют в виде 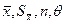 при доверительной вероятности
при доверительной вероятности 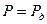 .
.
Идентификация формы распределения результатов измерений
В качестве способа оценки близости распределения выборки экспериментальных данных к принятой аналитической модели за кона распределения используются критерии согласия. Известен целый ряд критериев согласия, предложенных разными авторами. Наибольшее распространение в практике получил критерий Пирсона. Идея этого метода состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенной на основе распределения, совпадение с которым определяется. Использование критерия Пирсона [3, 48] возможно при большом числе измерений (n > 50) и заключается в вычислении величины 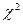 (хи-квадрат):
(хи-квадрат):
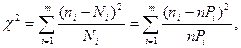
где 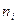 ,
, 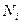 — экспериментальные и теоретические значения частот в i-м интервале разбиения; m — число интервалов разбиения; Pi — значения вероятностей в том же интервале разбиения, соответствующие выбранной модели распределения;
— экспериментальные и теоретические значения частот в i-м интервале разбиения; m — число интервалов разбиения; Pi — значения вероятностей в том же интервале разбиения, соответствующие выбранной модели распределения; 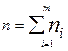 .
.
При 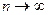 случайная величина
случайная величина 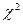 имеет распределение Пирсона с числом степеней свободы v = m-1-r, где r — число определяемых по статистике параметров, необходимых для совмещения модели и гистограммы. Для нормального закона распределения r = 2, так как закон однозначно характеризуется указанием двух его параметров — математического ожидания и СКО.
имеет распределение Пирсона с числом степеней свободы v = m-1-r, где r — число определяемых по статистике параметров, необходимых для совмещения модели и гистограммы. Для нормального закона распределения r = 2, так как закон однозначно характеризуется указанием двух его параметров — математического ожидания и СКО.
Если бы выбранная модель в центрах всех m столбцов совпадала с экспериментальными данными, то все m разностей 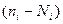 были бы равны нулю, а следовательно, и значение критерия
были бы равны нулю, а следовательно, и значение критерия 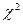 также было бы равно нулю. Таким образом,
также было бы равно нулю. Таким образом, 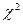 есть мера суммарного отклонения между моделью и экспериментальным распределением.
есть мера суммарного отклонения между моделью и экспериментальным распределением.
Критерий 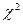 не инвариантен к числу столбцов и существенно возрастает с увеличением их числа. Поэтому для использования его при разном числе столбцов составлены таблицы квантилей распределения
не инвариантен к числу столбцов и существенно возрастает с увеличением их числа. Поэтому для использования его при разном числе столбцов составлены таблицы квантилей распределения 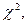 входом в которые служит так называемое число степеней свободы v = (m-1-r). Чтобы совместить модель, соответствующую нормальному закону, с гистограммой, необходимо совместить координату центра, а для того, чтобы ширина модели соответствовала ширине гистограммы, ее нужно задать как г = 2 и v = m—3. Часть квантилей распределения
входом в которые служит так называемое число степеней свободы v = (m-1-r). Чтобы совместить модель, соответствующую нормальному закону, с гистограммой, необходимо совместить координату центра, а для того, чтобы ширина модели соответствовала ширине гистограммы, ее нужно задать как г = 2 и v = m—3. Часть квантилей распределения 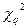 приведена в Если вычисленная по опытным данным мера расхождения
приведена в Если вычисленная по опытным данным мера расхождения 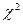 меньше определенного из таблицы значения
меньше определенного из таблицы значения 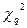 , то гипотеза о совпадении экспериментального и выбранного теоретического распределений принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. она не противоречит
, то гипотеза о совпадении экспериментального и выбранного теоретического распределений принимается. Это не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. она не противоречит
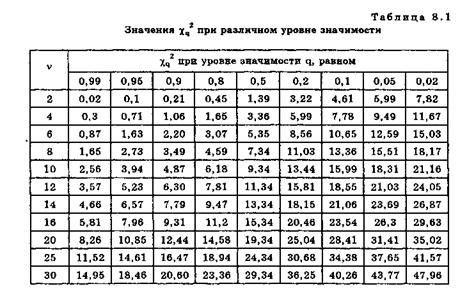
опытным данным. Если же 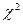 выходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным.
выходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным.
Методика определения соответствия экспериментального и принятого законов распределения заключается в следующем:
• определяют оценки среднего арифметического значения 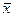 и СКО Sx по формулам (6.9) и (6.11);
и СКО Sx по формулам (6.9) и (6.11);
• группируют результаты многократных наблюдений по интервалам длиной h, число которых определяют так же, как и при
построении гистограммы;
• для каждого интервала разбиения определяют его центр xio и
подсчитывают число наблюдений ni попавших в каждый интервал;
вычисляют число наблюдений для каждого из интервалов,
теоретически соответствующее выбранной аналитической модели распределения. Для этого сначала от реальных середин интервалов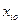 производят переход к нормированным серединам
производят переход к нормированным серединам 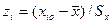 . Затем для каждого значения zi с помощью аналитической модели находят значение функции плотности вероятностей f(
. Затем для каждого значения zi с помощью аналитической модели находят значение функции плотности вероятностей f(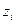 ).
).
По найденному значению f(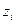 ) определяют ту часть
) определяют ту часть 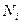 ; имеющихся наблюдений, которая теоретически должна быть в каждом из интервалов
; имеющихся наблюдений, которая теоретически должна быть в каждом из интервалов 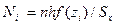 , где n — общее число наблюдений;
, где n — общее число наблюдений;
• если в какой-либо интервал теоретически попадает меньше
пяти наблюдений, то в обеих гистограммах его соединяют с сосед
ним интервалом. После этого определяют число степеней свободы
v = m-1-r, где m — общее число интервалов. Если было произведено укрупнение, то m — число интервалов после укрупнения;
• по формуле (8.1) определяют показатель разности частот 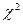 ;
;
• выбирают уровень значимости критерия q. Он должен быть
небольшим, чтобы была мала вероятность совершить ошибку первого рода. По уровню значимости и числу степеней свободы v по табл. 8.1 находят границу критической области 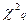 , такую, что
, такую, что 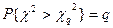 . Вероятность того, что полученное значение
. Вероятность того, что полученное значение  2 превышает
2 превышает 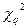 , равна q и мала. Поэтому, если оказывается, что
, равна q и мала. Поэтому, если оказывается, что 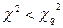 , то гипотеза о совпадении экспериментального и теоретического законов распределения отвергается. Если же
, то гипотеза о совпадении экспериментального и теоретического законов распределения отвергается. Если же 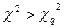 , то гипотеза принимается.
, то гипотеза принимается.
Чем меньше q, тем больше значение 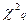 (при том же числе степеней свободы v), тем легче выполняется условие
(при том же числе степеней свободы v), тем легче выполняется условие 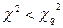 принимается проверяемая гипотеза. Но при этом увеличивается вероятность ошибки второго рода. В связи с этим нецелесообразно принимать 0,02 < q < 0,01.
принимается проверяемая гипотеза. Но при этом увеличивается вероятность ошибки второго рода. В связи с этим нецелесообразно принимать 0,02 < q < 0,01.
Иногда вместо проверки с односторонней критической областью применяют проверки с двусторонними критическими областями. При
этом оценивается вероятность P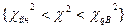 = q. Уровень значимости критерия q делится на две части:
= q. Уровень значимости критерия q делится на две части:  . Как правило, принимают
. Как правило, принимают 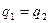 . По табл. 8.1 для P(
. По табл. 8.1 для P(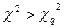 } = q находят
} = q находят 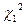 при уровне значимости
при уровне значимости 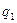 и числе степеней свободы v и
и числе степеней свободы v и 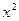 для уровня значимости 1 — q2 и том же n. Гипотеза о совпадении распределений принимается, если
для уровня значимости 1 — q2 и том же n. Гипотеза о совпадении распределений принимается, если 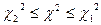 .
.
Однократные измерения
Прямые многократные измерения в большей мере относятся к лабораторным измерениям. Для производственных процессов более характерны однократные измерения. Однократные прямые измерения являются самыми массовыми и проводятся, если: при измерении происходит разрушение объекта измерения, отсутствует возможность повторных измерений, имеет место экономическая целесообразность. Эти измерения возможны лишь при определенных условиях:
• объем априорной информации об объекте измерений такой,
что модель объекта и определение измеряемой величины не вызы
вают сомнений;
• изучен метод измерения, его погрешности либо заранее устра
нены, либо оценены;
• средства измерений исправны, а их метрологические характе
ристики соответствуют установленным нормам.
За результат прямого однократного измерения принимается полученная величина. До измерения должна быть проведена априорная оценка составляющих погрешности с использованием всех доступных данных. При определении доверительных границ погрешности результата измерений доверительная вероятность принимается, как правило, равной 0,95.
Методика обработки результатов прямых однократных измерений приведена в рекомендациях МИ 1552—86 "ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений". Данная методика применима при выполнении следующих условий: составляющие погрешности известны, случайные составляющие распределены по нормальному закону, а неисключенные систематические, заданные своими границами 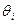 — равномерно.
— равномерно.
Составляющими погрешности прямых однократных измерений являются:
• погрешности СИ, рассчитываемые по их метрологическим характеристикам;
• погрешность используемого метода измерений, определяемая на основе анализа в каждом конкретном случае;
• личная погрешность, вносимая конкретным оператором.
Если последние две составляющие не превышают 15% погрешности СИ, то за погрешность результата однократного измерения принимают погрешность используемого СИ. Данная ситуация весьма часто имеет место на практике.
Названные составляющие могут состоять из неисключенных систематических и случайных погрешностей. При наличии нескольких систематических погрешностей, заданных своими границами ±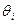 либо доверительными границами ±
либо доверительными границами ±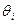 (Р), доверительная граница результата измерения соответственно может быть рассчитана по формуле
(Р), доверительная граница результата измерения соответственно может быть рассчитана по формуле
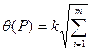
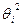 или
или 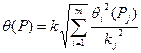
где 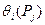 — доверительная граница i-й неисключенной систематической погрешности, соответствующая доверительной вероятности
— доверительная граница i-й неисключенной систематической погрешности, соответствующая доверительной вероятности 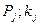 — коэффициент, зависящий от
— коэффициент, зависящий от 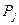 и определяемый так же, как и коэффициент k; k = k(m,P) — коэффициент, равный 0,95 при Р= 0,9 и 1,1 при Р = 0,95. При других доверительных вероятностях он определяется в соответствии с ГОСТ 8.207-76.
и определяемый так же, как и коэффициент k; k = k(m,P) — коэффициент, равный 0,95 при Р= 0,9 и 1,1 при Р = 0,95. При других доверительных вероятностях он определяется в соответствии с ГОСТ 8.207-76.
Случайные составляющие погрешности результата измерений выражаются либо своими СКО 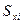 , либо доверительными границами
, либо доверительными границами 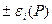 . В первом случае доверительная граница случайной составляющей погрешности результата прямого однократного измерения определяется через его СКО
. В первом случае доверительная граница случайной составляющей погрешности результата прямого однократного измерения определяется через его СКО 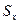 :
:

где 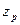 — точка нормированной функции Лапласа, отвечающей вероятности Р. При Р = 0,95
— точка нормированной функции Лапласа, отвечающей вероятности Р. При Р = 0,95 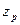 = 2. Если СКО
= 2. Если СКО 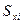 определены экспериментально при небольшом числе измерений (n < 30), то в данной формуле вместо коэффициента
определены экспериментально при небольшом числе измерений (n < 30), то в данной формуле вместо коэффициента 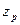 следует коэффициент Стьюдента, соответствующий числу степеней свободы i-й составляющей, оценка которой произведена при наименьшем числе измерений.
следует коэффициент Стьюдента, соответствующий числу степеней свободы i-й составляющей, оценка которой произведена при наименьшем числе измерений.
В случае, когда случайные погрешности представлены доверительными границами 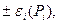 соответствующими разным доверительным вероятностям
соответствующими разным доверительным вероятностям 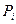 доверительная граница случайной погрешности результатов прямых однократных измерений
доверительная граница случайной погрешности результатов прямых однократных измерений
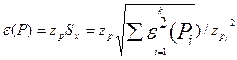 .
.
Найденные значения 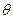 и
и 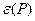 используются для оценки погрешности результата прямых однократных измерений. В зависимости от соотношения
используются для оценки погрешности результата прямых однократных измерений. В зависимости от соотношения 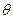 и
и 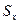 суммарная погрешность определяется по одной из формул, приведенных в табл. 8.2.
суммарная погрешность определяется по одной из формул, приведенных в табл. 8.2.
Значения коэффициента 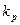 приведены в табл. 8.3.
приведены в табл. 8.3.
Таблица 8.2
Формулы для расчёта погрешности результата
прямых однократных измерений 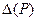
Значения 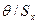
| Погрешность результата
измерения 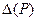
|
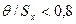
| 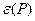
|
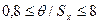
| 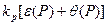
|
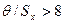
| 
|
Таблица 8.3
Значение 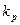 в зависимости от отношения
в зависимости от отношения 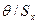 при доверительной вероятности 0,95
при доверительной вероятности 0,95
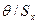
| 0,8 | ||||||||
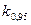
| 0,76 | 0,74 | 0,71 | 0,73 | 0,76 | 0,78 | 0,79 | 0,80 | 0,81 |
Кроме изложенного метода, суммирование случайных и систематических составляющих может производится и другими методами.
Результат прямых однократных измерений должен записываться в соответствии с рекомендациями МИ 1317-86 в виде 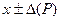 при доверительной вероятности
при доверительной вероятности 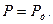
Выше были рассмотрены прямые однократные измерения с точным оцениваем погрешностей, наиболее детально они проана лизированы в [3]. В практике также имеют место прямые однократные измерения с приближенным оцениванием погрешности. Для них характерно оценивание погрешности полученного результата на основе метрологических характеристик, приведенных в нормативно-технической документации на используемые средства измерений. Поскольку эти характеристики относятся к любым экземплярам данного типа СИ, то у конкретного используемого средства действительные метрологические характеристики могут отличаться от нормированных.
Прямые однократные измерения с приближенным оцениванием погрешностей правомочны, если доказана возможность пренебрежения случайной составляющей погрешности измерения, т.е. можно обосновано считать, что среднее квадратическое отклонение 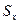 случайной составляющей меньше 1/8 суммарной границы неисключенных систематических составляющих погрешности результата измерения.
случайной составляющей меньше 1/8 суммарной границы неисключенных систематических составляющих погрешности результата измерения.
В простейшем случае, когда влияющие величины соответствуют нормальным условиям, погрешность результата прямого однократного измерения равна пределу основной погрешности средства измерения 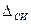 , определяемой по нормативно-технической документации. Результат измерения запишется в виде
, определяемой по нормативно-технической документации. Результат измерения запишется в виде 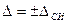 .Доверительная вероятность не указывается, но, как правило, подразумевается, что она равна 0,95. При проведении измерений в условиях, отличных от нормальных» необходимо определять и учитывать пределы дополнительных погрешностей. Возможная методика суммирования основных и дополнительных погрешностей однократных измерений приведена в [3].
.Доверительная вероятность не указывается, но, как правило, подразумевается, что она равна 0,95. При проведении измерений в условиях, отличных от нормальных» необходимо определять и учитывать пределы дополнительных погрешностей. Возможная методика суммирования основных и дополнительных погрешностей однократных измерений приведена в [3].
Пример 8.1. Оценить погрешность результата однократного измерения напряжения U = 0,9 В на сопротивлении R = 4 Ом, выполненного вольтметром класса точности 0,5 с верхним пределом измерения 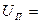 1,5 В а внутренним сопротивлением
1,5 В а внутренним сопротивлением 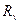 =1000 Ом. Известно, что дополнительные погрешности показаний вольтметра из-за магнитного поля и температуры не превышают соответственно
=1000 Ом. Известно, что дополнительные погрешности показаний вольтметра из-за магнитного поля и температуры не превышают соответственно 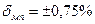 и
и 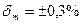 допускаемой предельной погрешности.
допускаемой предельной погрешности.
Предел допускаемой относительной погрешности вольтметра на отметке 0,9 В составляет 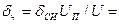 0,83%. При подсоединении вольтметра исходное напряжение
0,83%. При подсоединении вольтметра исходное напряжение 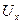 , изменится из-за наличия и составит
, изменится из-за наличия и составит
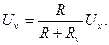
Тогда методическая погрешность, обусловленная конечным значением Rv, в относительной форме
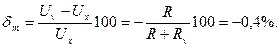
Данная погрешность является систематической и должна быть внесена в результат в виде поправки 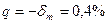 или в абсолютной форме на отметке 0,9 В
или в абсолютной форме на отметке 0,9 В 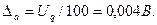 Тогда результат измерения с учетом поправки
Тогда результат измерения с учетом поправки 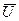 = 0,9 + 0,004 = 0,904В.
= 0,9 + 0,004 = 0,904В.
Поскольку основная и дополнительная погрешности заданы своими граничными значениями, то они могут рассматриваться как неисключенные систематические погрешности и соответственно суммироваться. При доверительной вероятности 0,95 доверительная граница неисключенной систематической погрешности
 = 1,1
= 1,1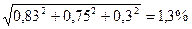 В абсолютной форме
В абсолютной форме 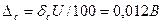 . Поскольку
. Поскольку 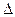 > q, то окончательный результат измерения записывается в виде
> q, то окончательный результат измерения записывается в виде 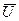 = 0,9 В;
= 0,9 В; 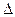 = ±0,01 В; Р = 0,95.
= ±0,01 В; Р = 0,95.
Косвенные измерения
Косвенные измерения — это измерения, при которых искомое значение Q находят на основании известной зависимости
Q =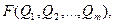 (8.2)
(8.2)
где 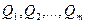 — значения, полученные при прямых измерениях. По виду функциональной зависимости F они делятся на две основные группы — линейные и нелинейные. Для линейных косвенных измерений математический аппарат статистической обработки полученных результатов разработан детально. Обработка результатов косвенных измерений [57] производится, как правило, методами: основанными на раздельной обработке аргументов и их погрешностей; линеаризации; приведения; перебора.
— значения, полученные при прямых измерениях. По виду функциональной зависимости F они делятся на две основные группы — линейные и нелинейные. Для линейных косвенных измерений математический аппарат статистической обработки полученных результатов разработан детально. Обработка результатов косвенных измерений [57] производится, как правило, методами: основанными на раздельной обработке аргументов и их погрешностей; линеаризации; приведения; перебора.
Первые три метода рассматриваются ниже, а четвертый — в [57]. Методика обработки результатов косвенных измерений приведена в документе МИ 2083—90 "ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей Косвенные измерения при линейной зависимости между аргументами. Линейная функциональная зависимость является простейшей формой связи между измеряемой величиной и находимыми посредством прямых измерений аргументами. Она может быть выражена формулой
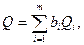
где 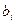 — постоянный коэффициент i-го аргумента
— постоянный коэффициент i-го аргумента 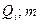 -число аргументов. Погрешности линейных косвенных измерений оцениваются методом, основанным на раздельной обработке аргументов и их погрешностей.
-число аргументов. Погрешности линейных косвенных измерений оцениваются методом, основанным на раздельной обработке аргументов и их погрешностей.
Если коэффициенты 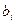 определяют экспериментально, то нахождение результата измерения величины Q производится поэтапно. Сначала оценивают каждое слагаемое
определяют экспериментально, то нахождение результата измерения величины Q производится поэтапно. Сначала оценивают каждое слагаемое 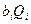 как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины Q. Результат косвенного измерения определяют по формуле
как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины Q. Результат косвенного измерения определяют по формуле
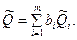
где 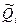 — оценка результата измерений аргумента
— оценка результата измерений аргумента 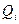 , получаемая, как правило, посредством обработки результатов многократных прямых измерений каждого из аргументов. При несмещенности и состоятельности результатов
, получаемая, как правило, посредством обработки результатов многократных прямых измерений каждого из аргументов. При несмещенности и состоятельности результатов 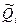 полученная оценка результата измерения
полученная оценка результата измерения 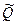 будет также несмещенной и состоятельной. Поскольку дисперсия результата измерения
будет также несмещенной и состоятельной. Поскольку дисперсия результата измерения
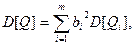
то, если результаты 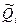 обладают минимальной дисперсией, т.е, являются эффективными, оценка результата измерения
обладают минимальной дисперсией, т.е, являются эффективными, оценка результата измерения 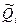 также будет эффективной.
также будет эффективной.
При отсутствии корреляционной связи между аргументами СКО результата косвенного измерения S(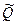 ), обусловленное случайными погрешностями, вычисляется по формуле
), обусловленное случайными погрешностями, вычисляется по формуле
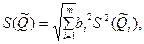
где S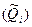 — среднее квадратическое отклонение результата измерения аргумента
— среднее квадратическое отклонение результата измерения аргумента 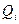 , рассчитываемое по формуле (6.10).
, рассчитываемое по формуле (6.10).
При наличии корреляционной связи между аргументами СКО результата косвенного измерения
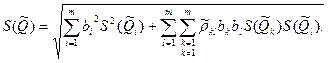
Здесь 
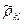 — несмещенная оценка коэффициента корреляции между погрешностями аргументов
— несмещенная оценка коэффициента корреляции между погрешностями аргументов 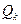 и
и 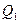 :
:
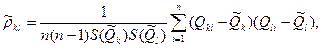
где 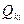 ,
, 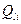 — i-e результаты прямых измерений k-гo и 1-го аргументов; n — число прямых измерений аргументов. Коэффициент корреляции может быть рассчитан и по другим формулам, равнозначным приведенной.
— i-e результаты прямых измерений k-гo и 1-го аргументов; n — число прямых измерений аргументов. Коэффициент корреляции может быть рассчитан и по другим формулам, равнозначным приведенной.
Корреляция между аргументами чаще всего возникает в тех случаях, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий (температуры, влажности, напряжения питающей сети, помех и т.п.). Критерием отсутствия связи между двумя аргументами является выполнение неравенства [48]
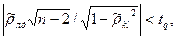
где 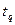 — коэффициент Стьюдента, соответствующий уровню значимости q и числу степеней свободы n-2. Необходимо проверить отсутствие корреляционных связей между всеми парными сочетаниями аргументов.
— коэффициент Стьюдента, соответствующий уровню значимости q и числу степеней свободы n-2. Необходимо проверить отсутствие корреляционных связей между всеми парными сочетаниями аргументов.
Моделью для распределения результатов измерений отдельных аргументов обычно можно считать случайную величину с нормальным распределением. Для распределений, отличных от нормального, распределение среднего арифметического при этом все же можно считать нормальным [3]. Случайную погрешность результата косвенного измерения, образующуюся путем сложения случайных погрешностей результатов определения многих аргументов, еще с большим основанием можно считать нормально распределенной случайной величиной. Это дает возможность найти доверительный интервал для значения измеряемой величины.
При большом числе измерений (более 25-30), выполненных при нахождении каждого из аргументов, доверительную границу случайной погрешности результата косвенного измерения можно определить по формуле
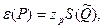

где 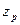 — квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р.
— квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р.
При меньшем числе измерений для определения доверительного интервала используется распределение Стьюдента, число степеней свободы которого рассчитывается по приближенной формуле [3]
F=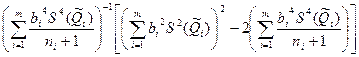 ,
,
где 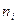 — число измерений при определении аргумента
— число измерений при определении аргумента 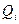 . В этом случае при условии, что распределение погрешностей результатов измерения аргументов не противоречит нормальному распределению, доверительная граница случайной погрешности результата косвенного измерения
. В этом случае при условии, что распределение погрешностей результатов измерения аргументов не противоречит нормальному распределению, доверительная граница случайной погрешности результата косвенного измерения
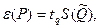
где 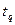 — коэффициент Стьюдента, соответствующий доверительной вероятности P=l-q и числу степеней свободы f.
— коэффициент Стьюдента, соответствующий доверительной вероятности P=l-q и числу степеней свободы f.
Систематическая погрешность результата косвенного измерения определяется систематическими погрешностями результатов измерений аргументов. При измерениях последние стремятся исключить. Однако полностью это сделать не удается, всегда остаются неисключенные систематические погрешности, которые рассматриваются как реализации случайной величины [57], имеющей равномерное распределение. Такое предположение приводит обычно к достаточно осторожным заключениям о погрешности результатов косвенных измерений.
Доверительные границы неисключенной систематической погрешности результата линейного косвенного измерения 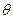 (Р) в случае, если неисключенные систематические погрешности аргументов заданы границами
(Р) в случае, если неисключенные систематические погрешности аргументов заданы границами 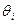 , вычисляют по формуле
, вычисляют по формуле
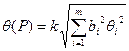 (8.4)
(8.4)
где k — поправочный коэффициент, определяемый принятой доверительной вероятностью Р и числом m составляющих 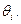 Его значения приведены в табл. 8.4. Погрешность от применения этих усредненных коэффициентов не превышает 10% [57].
Его значения приведены в табл. 8.4. Погрешность от применения этих усредненных коэффициентов не превышает 10% [57].
Таблица 8.4
Значения коэффициента к при m>4
| P | 0,90 | 0,95 | 0,98 | 0,99 |
| k | 0,95 | 1,1 | 1,3 | 1,4 |
Если число суммируемых слагаемых m < 4 и они значительно различаются между собой, то значение коэффициента k определяется по табл. 8.5. Под L здесь понимают отношение наибольшей длины интервала  одного из слагаемых к длине
одного из слагаемых к длине 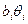 остальных слагаемых.
остальных слагаемых.
Если границы неисключенных систематических погрешностей результатов измерений аргументов заданы их доверительными границами 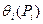 , соответствующими вероятностям
, соответствующими вероятностям 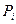 , то границу
, то границу  определяют по формуле
определяют по формуле
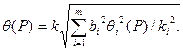
Таблица 8.5
| L | P=0,98 | P=0,99 | ||||
| m=2 | m=3 | m=4 | m=2 | m=3 | m=4 | |
| 1,22 | 1,28 | 1,30 | 1,28 | 1,38 | 1,41 | |
| 1,16 | 1,23 | 1,26 | 1,22 | 1,31 | 1,36 | |
| 1,11 | 1,17 | 1,20 | 1,16 | 1,24 | 1,28 | |
| 1,07 | 1,12 | 1,15 | 1,12 | 1,18 | 1,22 | |
| 1,05 | 1,09 | 1,12 | 1,09 | 1,14 | 1,18 |
Значения коэффициента к при m=2,3,4 Коэффициенты 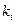 определяются так же, как поправочный коэффициент к.
определяются так же, как поправочный коэффициент к.
Суммарная погрешность результата косвенного измерения оценивается на основе композиции распределений случайных и неисключённых систематических погрешностей. Формулы для её расчёта в зависимости от соотношения границ неисключённой систематической составляющей и СКО случайной составляющей погрешности приведены в табл. 8.6.
Таблица 8.6
Погрешность результата косвенных измерений 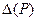
Значение 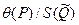
| Погрешность результата измерения 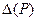
|
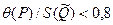
| 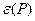
|
0,8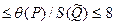
| 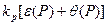
|
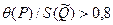
| 
|
Коэффициент 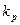 определяется по табл.8.7.
определяется по табл.8.7.
Результат косвенных измерений должен записываться в виде 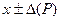 при доверительной вероятности P.
при доверительной вероятности P.
Косвенные измерения при нелинейной зависимости между аргументами. Для обработки результатов измерений при нелинейных зависимостях между аргументами некоррелированных погрешностях используется метод линеаризации. Он состоит в том, что нелинейная функция, связывающая измеряемую величину с аргументами разлагается в ряд Тейлора:
Таблица 8.7
Зависимость 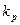 от отношения
от отношения 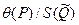 при различной доверительной вероятности
при различной доверительной вероятности
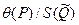
| 0,5 | 0,75 | ||||||||
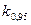
| 0,81 | 0,77 | 0,74 | 0,71 | 0,73 | 0,76 | 0,78 | 0,79 | 0,80 | 0,81 |
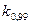
| 0,87 | 0,85 | 0,82 | 0,80 | 0,81 | 0,82 | 0,83 | 0,83 | 0,84 | 0,85 |
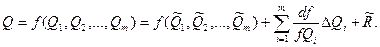 (8.5)
(8.5)
Здесь 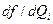 — первая частная производная от функции f по аргументу
— первая частная производная от функции f по аргументу 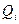 , вычисленная в точке
, вычисленная в точке 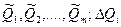 — отклонение результата измерения аргумента
— отклонение результата измерения аргумента 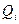 от его среднего арифметического;
от его среднего арифметического; 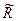 — остаточный член:
— остаточный член:
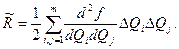
Метод линеаризации применим, если остаточным членом можно пренебречь. Это возможно в том случае, если
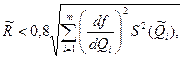
где S(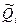 )— СКО случайной погрешности результата измерений аргумента
)— СКО случайной погрешности результата измерений аргумента 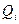 . При необходимости результаты косвенных измерений можно уточнить, используя члены ряда Тейлора более высокого порядка. Эти вопросы детально рассмотрены в [57].
. При необходимости результаты косвенных измерений можно уточнить, используя члены ряда Тейлора более высокого порядка. Эти вопросы детально рассмотрены в [57].
Оценка результата определяется по формуле
 (8.6)
(8.6)
Абсолютная погрешность косвенного измерения  , как это следует из уравнения (8.5), равна
, как это следует из уравнения (8.5), равна
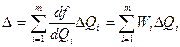
где 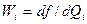 — коэффициенты влияния i-го аргумента;
— коэффициенты влияния i-го аргумента; 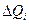 -абсолютная погрешность измерения 1-го аргумента;
-абсолютная погрешность измерения 1-го аргумента; 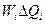 - частная i-я погрешность определения результата косвенного измерения.
- частная i-я погрешность определения результата косвенного измерения.
Пример 8.2. Разложить в ряд Тейлора уравнение для определения плотности и получить выражение для расчета абсолютной погрешности.
Плотность твердого тела  определяется как отношение результата измерения его массы m к объему V. При этом в соответствии с (8.5) получаем выражение
определяется как отношение результата измерения его массы m к объему V. При этом в соответствии с (8.5) получаем выражение
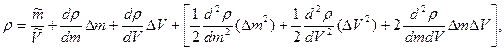
где в скобках стоит остаточный член. Учитывая, что
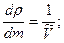
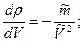
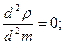
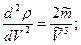
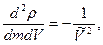
окончательно получим
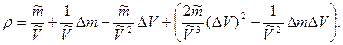
Абсолютная погрешность
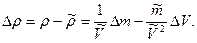
Коэффициенты влияния чаще всего определяются путем подстановки в выражения для частных производных оценок 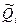 . Поэтому вместо самих коэффициентов влияния получаются их оценки. В ряде случаев они устанавливаются экспериментально, что приводит к возникновению еще одной погрешности нелинейных косвенных измерений. Этой погрешности можно избежать, если зависимость (8.1) имеет вид
. Поэтому вместо самих коэффициентов влияния получаются их оценки. В ряде случаев они устанавливаются экспериментально, что приводит к возникновению еще одной погрешности нелинейных косвенных измерений. Этой погрешности можно избежать, если зависимость (8.1) имеет вид
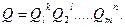
Тогда коэффициенты влияния
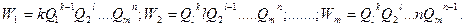
Оценка измеряемой величины находится по (8.6), (8.7), а ее относительная погрешность с учетом последних формул определяется как
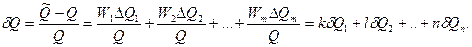
Из полученной формулы видно, что коэффициенты влияния для относительной погрешности оказываются равными показателям степеней соответствующих аргументов. Последние известны точно, и отмеченная выше погрешность не возникает. Для рассмотренного выше примера измерения плотности тела имеем 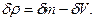
Оценка СКО случайной погрешности результата косвенного измерения
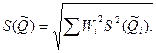 (8.8)
(8.8)
При точно известных коэффициентах влияния оно совпадает с уравнением (8.3), полученным для линейных косвенных измерений. Для зависимости вида (8.7) данная оценка, представленная в относительной форме, запишется в виде
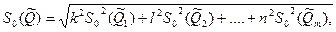
где 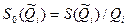 — оценка СКО i-го аргумента, представленная в относительной форме.
— оценка СКО i-го аргумента, представленная в относительной форме.
Доверительные границы случайной погрешности результата при нормально распределенных погрешностях измерений аргументов вычисляются так же, как и для линейных косвенных измерений, при условии, что вместо коэффициентов 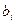 в формулах подставляются коэффициенты влияния
в формулах подставляются коэффициенты влияния 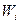 . Аналогичным образом поступают при определении границ неисключенной систематической погрешности. Погрешность результата нелинейных косвенных измерений оценивается так же, как и при линейных измерениях Метод приведения. Он используется для определения результатов косвенного измерения и его погрешности при наличии корреляции между погрешностями измерений аргументов. Метод можно также применять при неизвестных распределениях погрешностей аргументов. Он предполагает наличие ряда согласованных результатов измерений аргументов
. Аналогичным образом поступают при определении границ неисключенной систематической погрешности. Погрешность результата нелинейных косвенных измерений оценивается так же, как и при линейных измерениях Метод приведения. Он используется для определения результатов косвенного измерения и его погрешности при наличии корреляции между погрешностями измерений аргументов. Метод можно также применять при неизвестных распределениях погрешностей аргументов. Он предполагает наличие ряда согласованных результатов измерений аргументов полученных в процессе многократных измерений. Согласованность результатов измерений означает либо одновременное их осуществление, либо то, что они выполнены над одним и тем же объектом и в одних и тех же условиях.
полученных в процессе многократных измерений. Согласованность результатов измерений означает либо одновременное их осуществление, либо то, что они выполнены над одним и тем же объектом и в одних и тех же условиях.
Метод основан на приведении отдельных значений косвенно измеряемой величины к ряду простых измерений. Получаемые сочетания отдельных аргументов подставляют в формулу (8.6) и вычисляют отдельные значения измеряемой величины 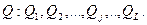
Результат косвенного измерения 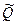 и СКО его случайной погрешности вычисляются по формулам
и СКО его случайной погрешности вычисляются по формулам
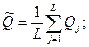
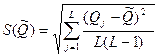
Доверительные границы случайной погрешности результата измерения рассчиталваются по формуле 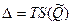 , где Т — коэффициент, зависящий от вида распределения отдельных значений определяемой величины и выбранной доверительной вероятности. При нормальном распределении отдельных значений измеряемой величины доверительные границы случайных погрешностей вычисляются по методике для прямых многократных измерений, изложенной в ГОСТ 8.207-76.
, где Т — коэффициент, зависящий от вида распределения отдельных значений определяемой величины и выбранной доверительной вероятности. При нормальном распределении отдельных значений измеряемой величины доверительные границы случайных погрешностей вычисляются по методике для прямых многократных измерений, изложенной в ГОСТ 8.207-76.
Границы неи
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 3080; Нарушение авторских прав?; Мы поможем в написании вашей работы!