Статистические ряды распределения

Простейшей группировкой является статистический ряд распределения.

Статистический ряд распределения – это упорядоченное распределение единиц изучаемой совокупности на группы по группировочному признаку. Ряды распределения принято оформлять в виде таблицы.

Различают атрибутивный и вариационный ряд распределения. Атрибутивные ряды распределения строятся по качественному признаку, а вариационные ряды по количественному.

Элементами атрибутивного ряда распределения являются качественный группировочный признак и число единиц совокупности в каждой группе.

Вариационный ряд представляет собой упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям группировочного признака с подсчетом числа совокупности по группам. Каждая группа вариационного ряда распределения характеризуется двумя элементами – вариантом и частотой.

Вариант– это числовое значение варьирующего признака, которое он принимает в ряду распределения.

Частота - численностью единиц отдельных вариантов или каждой группы вариационного ряда. Сумма частот составляет объем ряда распределения или общее количество варьируемых признаков. Доля частоты или удельный вес частоты каждой группы в общем объеме ряда распределения называется частостью. Частости выражаются в долях единицы, если сумма частот принимается за единицу, или в процентах, если сумма частот принимается за 100 %.

Для характеристики ряда распределения и расчета отдельных показателей используются также величины накопленной частоты (кумуляты) и накопленной частости.

Накопленная частота показывает сколько значений признака наблюдалось со значением равным или меньше рассматриваемого. Накопленная частота отдельных групп кроме того показывает ранг (порядковый номер) последнего значения признака в рассматриваемой группе.

Различают два вида вариационных рядов распределения – дискретный и интервальный.

Вариационный дискретный ряд распределения строится на основе признака с прерывной вариацией – дискретной величины. К дискретным величинам относятся целые значения признака, например, число детей в семье, число сидячих мест в автобусах и т.п.

Группировочным признаком в интервальных рядах распределения является непрерывно изменяющаяся величина, то есть величина, принимающая как целые, так и дробные значения. Поэтому варианты представлены в интервалах. Интервалом называется числовые значения признака (варианты) в определенных границах. У каждого интервала имеется нижняя и верхняя граница. Нижняя граница – это минимальное значение в интервале. Верхняя граница – максимальное значение в интервале. Разница между границами называется величиной или шагом интервала. Шаг интервала может быть одинаковым и разным. Если шаг интервала одинаковый, считает, что ряд распределения состоит из равных интервалов. Интервалы с разным шагом называют неравными. Так, в таблице 3.4. шаг второго интервала равен 9 (10 - 1), а третьего интервала – 40 (50 – 10) млрд. куб.м.

Таблица 3.4.

Группировка предприятий по объемам годовой добычи природного

газа в России в 1995 г.

Объем годовой добычи газа, млрд. куб. м	Количество предприятий, единиц
До 1
1 - 10
10 - 50
Свыше 50
Итого

Интервальная группировка с равными интервалами строится в следующем порядке:

1) все единицы совокупности распределяются в порядке возрастания или убывания (ранжируются);

2) определяется число групп, если оно не задано, по формуле Стерджесса:

n = 1 + 3.322 lg N,

где n – число групп;

N – численность единиц статистической совокупности.

3) рассчитывается шаг интервала:

х _мах – х _min

h = ─────────,

n

Значения шага интервала округляются в большую сторону.

3) определяются границы интервалов. В качестве нижней границы первого интервала берется минимальное значение признака. К нему прибавляют шаг интервала и получают верхнюю границу первого интервала, которая одновременно является нижней границей второго интервала. К ней прибавляется шаг интервала и получают верхнюю границу второго интервала, которая в то же время является нижней границей третьего интервала и т.д.:

первый интервал х _min - (х _min + h);

второй интервал (х _min + h) - (х _min + 2 h);

третий интервал (х _min + 2 h) - (х _min + 3 h) и т.д.;

4) все единицы совокупности распределяются по интервалам и подсчитываются частоты f _i в каждом интервале.

Интервалы могут закрытыми и открытыми. Закрытыми являются интервалы, имеющие обе границы. Границы закрытых интервалов могут оформляться в виде записей "от 5 до 10, от 10 до 15" или "5 -10", "10 - 15".

Открытыми бывают первый и последний интервалы. У первого интервала отсутствует нижняя граница (до 5, до 10), у последнего – верхняя (15 и более). Но для определения середины интервала требуется знать обе границы. Середина интервала равна половине суммы границ интервала. Чтобы определить неизвестную границу открытого интервала, необходимо сначала приравнять шаг открытого интервала шагу смежного интервала. Шаг первого интервала будет равен шагу второго, а шаг последнего – шагу предпоследнего интервала. Нижнюю границу первого интервала находят путем вычитания от верхней границы шага интервала, верхнюю границу последнего интервала – путем сложения нижней границы с шагом интервала.

Нижняя граница первого интервала должна охватывать минимальное значение варьирующего признака. Верхняя граница последнего интервала должна быть такой, чтобы в интервал вошло максимальное значение признака.

При совпадении числовых значений признака с какой-либо границей какого-то интервала формирование границ осуществляется по принципу "исключительно" (или "включительно"): числовые значения, обозначающие верхние границы исключается из рассматриваемого интервала, а включается в следующий интервал. Например, в интервале "от 5 до 10" число 10 по этому принципу не входит в данный интервал, а включается в следующий - "от 10 до 15", соответственно число 15 также не входит в интервал от "10 до 15", а включается в следующий - "от 15 до 20".

Когда признак варьирует в значительных размерах и неравномерно, применяются неравные интервалы. Неравные интервалы могут быть прогрессивно возрастающими в арифметической и геометрической прогрессии:

aрифметическая прогрессия h _i+1= h_i + a,

геометрическая прогрессия h _i+1= h_i *q,

где а – константа, число которое будет положительным при прогрессивно возрастающих интрвалах и отрицательным – при прогрессивно убывающих интервалах;

q – константа, положительное число, которое при прогрессивно возрастающих интервалах будет больше 1, а при прогрессивно убывающих интервалах – меньше 1.

Закономерности варьирования признаков можно представить графически.

Для дискретного ряда распределения график распределения признака называется полигоном распределения, интервального ряда – гистограмма кумулятивного ряда (по накопленным частотам) – кумулятивная кривая или кумулята.

Например, график дискретного ряда, оформленного в таблице 3.5, представлен на рис. 3.2.

Таблица 3.5

Распределение семей по числу детей в семье

Число детей в семье, чел.	Число семей
Итого

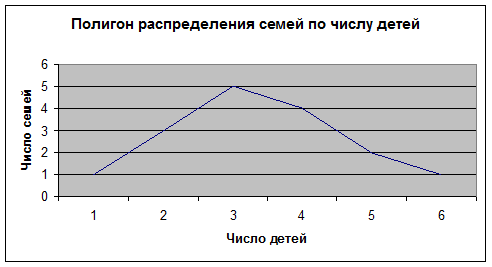
Рис. 3.1. Полигон распределения семей по числу детей

Гисторамма, изображающая интервальный ряд, представляет собой сомкнутые столбики, ширина которых равна шагу интервала, а высота – частоте интервалов.

Дата добавления: 2014-01-20