Среднее квадратичное отклонение, доверительный интервал и доверительная вероятность. Статистическая обработка экспериментальных результатов

Список рекомендуемой литературы

- 1. Хенли Е.Дж., Кумамото Х. Надійність проектування технічних систем і оцінка риску. – К.: Вища школа, 1987 – 544 с.

2. Ильин Ю.А. Расчёт надёжности подачи воды. – М.: Стройиздат, 1987 – 320 с.

- 3. Половко А.М., Маликов И.М., Жигарев А.Н., Зарудный В.И. Сборник задач по теории надёжности. – М.: Советское радио, 1977 – 408 с.

Лекция №2

Некоторые сведения из теории вероятностей и математической статистики. Оценка надёжности экспериментальных данных.

Теория надёжности использует для своих расчётов аппарат теории вероятностей. Вспомним некоторые сведения теории вероятностей и математической статистики, которые могут быть полезны в данном курсе.

Вероятность события С выражается зависимостью

,

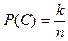где k- число благоприятных случаев, приводящих к событию С; n- общее число случаев.

Если события С и D входят в одну группу случаев, но взаимно исключают друг друга, то вероятность того, что одно какое-нибудь из них произойдёт равна сумме вероятностей . Следствием этого является то, что сумма вероятностей полной группы случаев равна 1.

Пример: бросание монетки, полная группа событий – орёл, решка или падение монетки на ребро. Пренебрегая вероятностью падения на ребро, получим: Р(орла)+Р(решки)=1

Если события С и D входят в одну группу случаев, независимы и не исключают друг друга, то вероятность того, что произойдут одновременно оба события равно произведению вероятностей

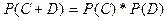
Например: вероятность удара молнии в высотное здание в Донбассе оценивается как 10^-8 , а вероятность неисправности молниеотвода условно оценим в 10^-5. Тогда вероятность поражения здания молнией равна произведению вероятностей, т.е. 10^-13.

Если события зависимы, то 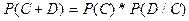, где - вероятность события D при условии, что событие С уже произошло. Пример: доставание разноцветных шариков из урны с небольшим числом шаров.

Забегая несколько вперёд, скажу, что надёжность работы сложных технических систем вычисляется как произведение вероятностей безотказной работы элементов системы, т.е. рассматривается как вероятность независимых не исключающих друг друга событий. Так, вероятность безотказной работы системы из 4-х элементов, каждый из которых имеет коэффициент безотказности 0,999 составит 0,999⁴ =0,996, т.е. существенно ниже, чем каждого элемента в отдельности.

Вероятность отказа каждого элемента определяется, как правило, по результатам экспериментальных данных. Поэтому необходимо научиться оценивать надёжность результатов эксперимента. Вы наверняка уже сталкивались с методикой такой оценки, поэтому здесь приведём эту методику в сокращенном виде и без теоретического обоснования.

Результаты эксперимента дают нам совокупность изменения случайной величины. Для обобщённой характеристики такой совокупности используют среднюю арифметическую 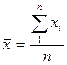, если имеются повторяющиеся варианты, то вычисляется средневзвешенная 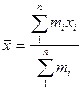, иногда используют среднюю геометрическую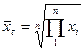

Для характеристики размаха колебаний применяют среднее квадратичное отклонение 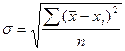, величина 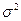называется дисперсией. При сравнении дисперсии различных величин пользуются относительной величиной – коэффициентом вариации V=

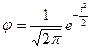Распределение случайных величин в природе чаще всего подчиняется нормальному закону , где t=, причём для функции составлены таблицы нормального распределения. Таким образом, можно рассчитать ожидаемую вероятность случайной величины при заданном значении t. На практике чаще поступают наоборот – указывают ожидаемое значение величины при заданной вероятности. Обычно в технике доверительную вероятность принимают равной 0,95, но при расчётах связанных с надёжностью ответственных систем принимается доверительная вероятность 0,99 и выше. При этом используют интервальную оценку величины , где - коэффициент, зависящий от доверительной вероятности (иногда его обозначают как t) и числа опытов, определяемый по специальным таблицам.

Лекция №3

Дата добавления: 2014-01-20