Диффузия примеси полупроводников

Для создания в полупроводнике слоев с различным типом проводимости и p-n переходов используются 2 метода введения примесей:

- термическая диффузия

- ионная имплантация (легирование)

Диффузия – это направленное движение атомов, возникшее под действием градиента концентрации или температуры.

В зависимости от условий протекания массы переноса, выделяют:

- взаимодиффузия (просто диффузия), которая наблюдается при наличии градиента концентрации или градиента химического потенциала.

- самодиффузия, протекает в отсутствие градиента.

Основные характеристики диффузных слоев:

1) глубина сопротивления, глубина залегания p-n перехода или легирующего слоя

2) поверхностное сопротивление или поверхностная концентрация примесей

3) распределения примесей в легируемом слое

Примеси, создаваемые в проводнике тот или иной тип проводимости, являются примесями замещения. Основными донорными примесями в кремнии являются элементы 5 группы таблицы Менделеева. Акцепторные элементы - 3 группы.

Большинство других образуют кремниевые растворы внедрения, то есть диффузирует по междоузлиям.

Математическое описание диффузионных процессов применительно к идеальным газам и растворам предложено Фиком.

Диффузия в твердых телах также подчинятся этим законам.

1 закон Фика устанавливает связь между плотностью потока диффузирующего вещества и градиентом концентрации.

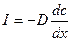- в одном направлении Х (в одномерном приближении)

D – коэффициент диффузии

c – концентрация атомов примеси

х – направление

Знак минус в данном направлении указывает на то, диффузионный поток направлен в сторону убывания концентрации. Коэффициент диффузии определяет плотность потока атомов вещества при заданном градиенте концентрации, так как диффузионный поток атомов вещества идет в направлении выравнивания перепада концентрации, то коэффициент D является мерой скорости, с которой система способна при заданных условиях выровнять разность концентраций. Эта скорость зависит только от плотности диффузионных атомов в кристаллической решетке полупроводника.

2 закон Фика описывает нестационарный процесс диффузии и выражает изменение концентрации диффузионного вещества в различных точках пространства, как функцию времени τ, для изометрической диффузионной среды он зависит как:

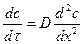
τ – время

D – константа

Полупроводниковая электроника широко оперирует с монокристаллическими объектами. Здесь в силу вступает закон об анизотропии и возникает необходимость учитывать влияние различных направлений на характер и результаты диффузии.

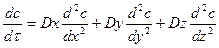
Dxyz – коэффициент диффузии в направлениях X, Y, Z → const

Диффузия – это активационный процесс и температурная зависимость коэффициентов диффузии подчиняется законам Аррениуса и выражается как:

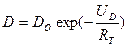, где 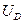= Дж/моль

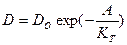, где А = ЭВ

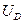=NA

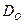- предэкстонециальный множитель

R – универсальная газовая постоянная

К – постоянная Больцмана

N – число Авогадро

Т – абсолютная температура

Дата добавления: 2014-01-20