Сделаем два предположения

1. Состояние (S_k) системы в конце K^-го шага зависит только от предшествующего состояния S_k-1 и управления на K^-м шаге Х_к (и не зависит от предшествующих состояний и управлений). Это требование называется "отсутствием последействия". Сформулированное положение записывается в виде уравнений

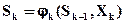, (2)

которые называются уравнениями состояний.

2. Целевая функция (1) является функцией от показателя эффективности каждого шага. Обозначим показатель эффективности K^-го шага через

, (3)

тогда

(4)

Задача динамического программирования пошаговой оптимизации формулируется так: определить такое допустимое управление X, переводящее систему S из состояния S₀ в состояние S₁, при котором целевая функция (4) принимает наибольшее (наименьшее) значение.

Выделим особенности модели динамического программирования:

- задача оптимизации интерпретируется как n- шаговый процесс управления;

- целевая функция равна сумме целевых функций каждого шага;

- выбор управления на k^-м шаге зависит только от состояния системы к этому шагу и не влияет на предшествующие шаги (нет обратной связи);

- состояние S_k после k^-го шага управления зависит только от предшествующего состояния S_k-1 и управления Х_к (отсутствие последействия);

- на каждом шаге управление Х_к зависит от конечного числа управляющих переменных, а состояние S_k - от конечного числа параметров.

Существуют различные способы решения подобных задач, применяемые в зависимости от вида функций, ограничений, размерности и т.

Принцип оптимальности, впервые сформулированный Р. Беллманом (в 1953г.), формулируется следующим образом: каково бы ни было состояние S системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Беллманом сформулированы и условия, при которых принцип верен. Основное требование - процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.

Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого под процесса по отношению к исходному состоянию этого под процесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.

В качестве исходной задачи динамического программирования с фиксированным числом шагов n и начальным состоянием S₀ можно рассматривать последовательность задач, полагая последовательно, n=1, 2,... при различных S - одношаговую, двухшаговую и т.д., - используя принцип оптимальности.

На каждом шаге любого состояния системы S_k-1 решение X_k нужно выбирать осторожно, так как этот выбор влияет на последующее состояние S_k и дальнейший процесс управления, зависящий от S_k. Это следует из принципа оптимальности.

Но есть один шаг, последний, который можно для любого состояния S_n-1 планировать локально-оптимально, исходя только из соображений этого шага.

Рассмотрим n -й шаг: S_n-1 - состояние системы к началу n -го шага, S_n= S_i -конечное состояние, X_n - управление на n -ом шаге, а (S_n-1, X_n) - целевая функция (выигрыш) n -го шага.

Согласно принципу оптимальности, X_n нужно выбирать так, чтобы для любых состояний S_n-1 получить максимум целевой функции на этом шаге.

Обозначим через (S_n-1) максимум целевой функции - показателя эффективности n -го шага при условии, что к началу последнего шага система S была в произвольном состоянии S_n-1, а на последнем шаге управление было оптимальным.

(S_n-1) называется условным максимумом целевой функции на n -м шаге и описывается равенством:

(5)

Решение (S_n-1), при котором достигается (S_n-1) называется условным оптимальным управлением на n -м шаге.

Задача будет двухшаговой, если присоединим к n -му шагу n-1

Для любых состояний S_n-2 , произвольных управлений X_n-1 и оптимальном управлении на n -м шаге значение целевой функции на двух последних шагах равно:

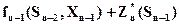(6)

Согласно принципу оптимальности для любых S_n-2 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (n-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (6) повсем допустимым управлениям X_n-1. Максимум этой суммы обозначим ее через 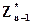(S_n-2) и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах. Соответствующее управление 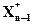(S_n-1) на (n - 1)-м шаге называется условным оптимальным управлением на (n -1)-м шаге.

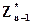(S_n-2)=

(7)

Выражение, состоящее в фигурных скобках (7), зависит только от s_n-2 и Х_n-1, так как s_n-1 можно найти из уравнения состояний (2) при k=n-1

s_n-1=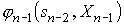
и подставить вместо s_n-1 в функцию(s_n-1).

В результате максимизации только по одной переменной X_n-1 согласно уравнению (7) вновь получаются две функции:

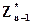(S_n-2) и 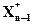(S_n-2)

Далее рассматривается трехшаговая задача: к двум последним шагам присоединяется (n-2)-й и т. д.

[1] Капитальные вложения – затраты материалов, труда и других ресурсов, направленные на восстановление и прирост основных фондов.

[2] Перевооружение – процесс повышения технического уровня производства путем внедрения новой техники, технологии, модернизации, замены, автоматизации производства.

[3] Интенсивный – отражает использование основных фондов, отражает уровень их использования по мощности (производительности.

[4] Экстенсивный – по времени.

[5] Априорный – с лат., независимый от опыта, предшествующий опыту.

[6] Функционалы – математическое понятие, для обозначения переменной величины, заданной на множестве функции.

[7] Вариация – от латинского изменение, - смещение независимого переменного или функционала.

Дата добавления: 2014-01-20