Проблема останова

Алгоритмически неразрешимые задачи

Универсальная функция

В теории алгоритмов установлен важный факт: во всех алгоритмических моделях всегда существует универсальный алгоритм.

Теорема: существует вычислимая функция двух аргументов u, являющаяся универсальной функцией для класса вычислимых функций одного аргумента.

Доказательство:

Расположим все программы, вычисляющие функции одного аргумента, в вычислимую последовательность p₀, p₁… (например, в порядке возрастания их длины).

Пусть u есть вычислимая функция, такая, что u (i;x) равна результату работы i- ой программы p_i на входном слове x.

Если программа p_i заканчивает работу на входном слове x, и не определена в противном случае (т.е. программа p_i не приемлема к входному слову x), то функция u и есть искомая двухместная универсальная вычислимая функция для классов всех одноместных вычислимых функций. (ч.т.д.)

Алгоритм, вычисляющий саму функцию u, есть, по существу, интерпретатор используемого языка программирования.

Ограниченность подхода «алгоритм = программа» состоит в том, что:

1) все, что можно запрограммировать с помощью какого-либо языка программирования, представляется любой из алгоритмических моделей;

2) формализация понятия алгоритма.

Требование (свойство) результативности алгоритма можно сформулировать так: построить алгоритм В, такой, что для любого алгоритма А В 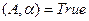, если 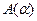дает результат, и В 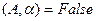, если 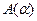не дает результата.

Теорема: не существует машины Тьюринга Т₀, решающей проблему останова для произвольной машины Тьюринга.

Следовательно, невозможно разработать программу для компьютера, решающую эту проблему. Такой результат принципиально невозможно получить, оставаясь в рамках программирования для компьютера.

Неразрешимость проблемы останова требует доказать сходимость предлагаемых алгоритмов, но показывает, что поиск таких доказательств нельзя полностью автоматизировать.

Дата добавления: 2014-01-20