Взвешенные графы

Взвешенные графы – графы, ребрам или дугам которых поставлены в соответствие числовые величины (более обобщенно – сеть).

Вес графа равен сумме весов его ребер. Вес ребра можно назвать и длиной.

V₂ 50 V₁

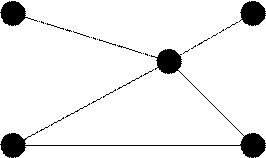
30 10

25 15 25

35 V₅

V₃ 50 V₄

Способы представления графов:

- списки смежности;

- матрица смежности;

- матрица инциденций.

Матрица смежности – это таблица, строки и столбцы которой соответствуют номерам вершин графа.

Если вершины смежные, то элементы матрицы смежности равны 1, иначе элементы матрицы равны 0. очевидно, что диагональные элементы матрицы равны нулю, так как вершины сами с собой не смежны.

	V1	V2	V3	V4	V5
V1
V2
V3
V4
V5

Матрица смежности неориентированного графа

	V1	V2	V3	V4	V5
V1
V2
V3
V4
V5

Матрица смежности взвешенного графа

Матрица инцидентности – прямоугольная матрица n*m, где n – количество вершин, m – количество ребер. Значение элементов матрицы определяется следующим образом: если ребро R _i и вершина V _j инцидентны, то значение соответствующего элемента матрицы равно 1, в противном случае значение равно нулю. Для орграфов матрица инциденций строится по следующему принципу: значение элемента равно 1, если ребро R _i исходит из вершины V _j, если ребро R _i заходит в вершину V _j, то значение равно 0.

	V1	V2	V3	V4	V5
R12
R14
R15
R23
R25
R34
R35

Матрица инциденций для неориентированного графа G (см. стр.)

Список смежности (инциденций) представляет собой структуру данных, которая для каждой вершины графа хранит список смежных с ней вершин. Список представляет собой массив указателей, i-ый элемент которого содержит указатель на список вершин, смежных с i-ой вершиной.

Список смежности более эффективен по сравнению с матрицей смежности, так как исключает хранение нулевых элементов.

V1	V2	V3	V4	V5
V2, V5 V4	V1,V3 V5	V2 , V4 V5	V1, V3 V5	V1, V2 V3, V4

Список смежности для неориентированного графа

7 апреля

СРС: 1. Добавить в таблицу «Методы сортировки» топологическую сортировку.

2. Написать алгоритм поиска в глубину.

Дата добавления: 2014-01-20