Определение 9.1

Правило трех сигм для случайной величины, распределенной по нормальному закону, формулируется так: отклонение случайной величины Х от ее ма-тематического ожидания практически не превышает ±3σ.

Практически достоверно, что величина распределения по нормальному закону отклоняется от математического ожидания не более чем на утроенное среднее квадратическое отклонение, т.е.

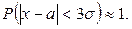
С меньшей степенью достоверности правило действует для х с произвольным знаком распределения, ибо справедлива оценка:

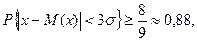
получающаяся из неравенства Чебышева, если положить в нем

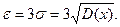
Серединным, или вероятным отклонением случайной величины называют такое число а₀, что вероятности неравенств

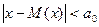и

одинаковы (т.е. равны по 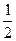каждая).

Вопросы для самоконтроля

1. Какая случайная величина называется величиной, распределенной по нормальному закону?

2. Какие величины являются параметрами нормального распределения?

3. Какие формулы используются для определения вероятности попадания случайной величины X в интервал от α до β?

4. Как формулируется правило трех сигм для нормально распределенной случайной величины?

5. Какая формула используется для расчета вероятности попадания нормально распределенной случайной величины в заданный интервал?

6. Какая формула использустся для определения вероятности попадания частоты случайной величины, распределенной по биномиальному закону в некоторый интервал?

7. В чем отличие формул, определяющих вероятность попадания частоты и частости (относительной частоты) случайной величины, распределенной по биномиальному закону, в некоторый интервал?

Дата добавления: 2014-01-20