Силовые линии электрического поля. Поток вектора напряженности электрического поля

Для наглядного представления электрического поля используют силовые линии.

Силовыми линиями (линиями напряженности) электрического поля называются линии, проведенные в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором напряженности поля (рис. 1.4.1).

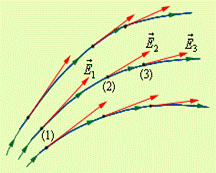
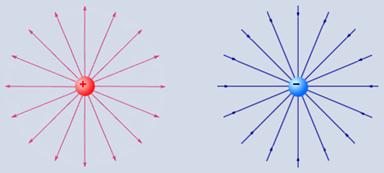
Рис. 1.4.1. Рис. 1.4.2.

На рис. 1.4.2 приведена картина силовых линий электрических полей положительного и отрицательного одиночных точечных зарядов.

Рис. 1.4.3.

На рис. 1.4.3. изображена картина силовых линий поля электрического диполя – системы из двух одинаковых по модулю зарядов разного знака +q и –q, расположенных на некотором расстоянии l. На этом рисунке показано, что вектор напряженности E поля, направленный по касательной к силовой линии, получается как сумма векторов напряженностей E ₁ и E ₂ каждого из точечных зарядов: .

Важной характеристикой электрического диполя является так называемый дипольный момент p:

, (1.4.1)

где l – вектор, направленный от отрицательного заряда к положительному, при этом его модуль равен 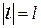. Диполь может служить электрической моделью многих молекул.

Свойства силовых линий.

1. Силовые линии электрического поля всегда начитаются на положительных и оканчиваются на отрицательных зарядах или уходят в бесконечность.

2. Силовые линии не пересекаются. В противном случае в точке пересечения было бы два различных вектора напряженности.

3. С помощью картины силовых линий можно определить не только направление вектора напряженности E, но и его величину по густоте силовых линий. Густота силовых линий в малой окрестности некоторой точки поля численно равна величине напряженности электрического поля.

Густотой силовых линий называется число силовых линий D N, проходящих через единичную площадку перпендикулярно к ней.

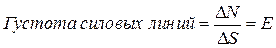. (1.4.2)

Во многих задачах электростатики требуется определить электрическое поле по заданному распределению зарядов. Для этого используется понятие потока вектора напряженности электрического поля.

Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка D S. Произведение модуля вектора напряженности E на площадь D S площадки и на косинус угла a между вектором E и нормалью n к площадке называется элементарным потоком вектора напряженности через площадку D S (рис. 1.4.4):

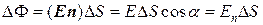, (1.4.3)

где E_n – модуль нормальной составляющей напряженности электрического поля E.

Рис. 1.4.4.

Из формул (1.4.2) и (1.4.3) следует, что модуль потока вектора напряженности равен числу силовых линий D N, проходящих через малую площадку перпендикулярно к ней: . Однако, в отличие от числа силовых линий, которое не может быть отрицательным, поток вектора напряженности может быть как отрицательным, так и положительным.

Дата добавления: 2014-01-20