
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Размерные цепи
|
|
|
|
Одним из самых эффективных методов расчета геометрических параметров составных частей конструкций, является метод размерных цепей. Метод позволяет устанавливать расчетом допуски и отклонения геометрических параметров или проверить правильность их назначения для обеспечения собираемости и работоспособности изделий.
Использование методов расчёта размерных цепей позволяют сократить как время так и материальные затраты на этапе технической подготовки и производства конструкций, повысить качество и сократить сроки отработки изделий, их конструкторской и технологической документации. Каждая размерная цепь имеет одно замыкающее звено. Замыкающими такие звенья называют потому, что в процессе сборки изделия или при обработке элементов отдельных деталей они замыкают реальную размерную цепь. Замыкающие звенья размерной цепи непосредственно не выполняются, а являются результатом выполнения (в том числе изготовления) всех других звеньев, составляющих размерную цепь. Применяемые методы достижения точности замыкающего звена, т.е. методы расчёта размерных цепей, показаны на Рисунке 1.
Любая размерная цепь имеет замыкающее звено и составляющие звенья размерной цепи. Из приведённых методов расчёта размерных цепей базовым можно считать «метод полной взаимозаменяемости», на основе которого получены основные определения и зависимости. Рассмотрение других методов после освоения «метода полной взаимозаменяемости» становится менее затруднительным.
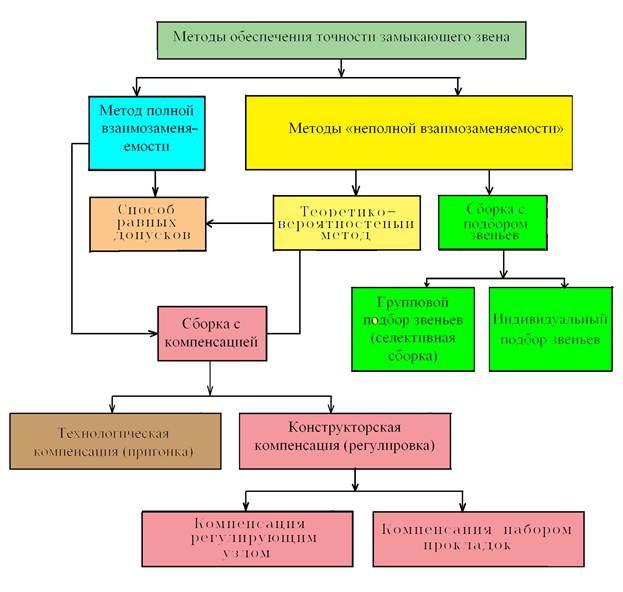
Рисунок 1. Методы обеспечения точности замыкающего звена
Основные определения и классификация размерных цепей
Размерной цепью называется совокупность взаимосвязанных размеров, определяющих взаимное расположение осей и поверхностей одной детали (детальная размерная цепь, рис. 2) или нескольких деталей в изделии (сборочная размерная цепь, рис.3), расположенных в определённой последовательности по замкнутому контуру и непосредственно влияющих на точность одного из размеров контура.
Каждая размерная цепь состоит из составляющих звеньев (размеров) цепи и замыкающего звена (размера). Геометрические схемы позволяют исключить возможность ошибок и упростить задачу выявления размерных цепей, особенно при сложных многозвенных цепях.
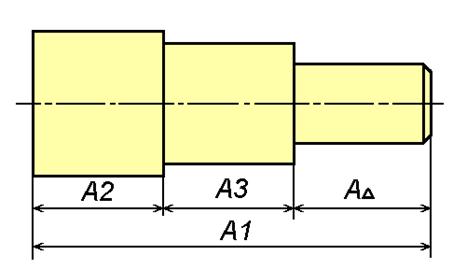
Замыкающим размером (АΔ; рис.2,3,4) называется размер, получающийся последним в процессе обработки детали или сборки узла, величина и точность которого зависят от величины и точности всех остальных размеров цепи, называемых составляющими (А1, A2...An-1; рис. 2, 3).
К числу основных типовых замыкающих звеньев размерных цепей относят:
- зазоры и натяги в сопряжениях деталей;
- выступы и перекрытия элементов одних деталей относительно других;
- симметричность поверхностей;
- зацепление поверхностей одних деталей относительно других;
- соосность цилиндрических поверхностей одной или нескольких деталей;
- расстояния между поверхностями деталей, определяющие начало и конец воздействия одной детали на другую.
Классификация звеньев размерных цепей размерных цепей показана в таблице 1.
По взаимному расположению размеров размерные цепи делятся на линейные, плоскостные и пространственные.
Линейными называются размерные цепи, звенья которых расположены параллельно друг другу (рис. 2, 3)
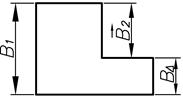
Плоскостными называются размерные цепи, все иличасть звеньев которых не параллельны друг другу, но расположены в одной или нескольких параллельных плоскостях (рис. 4).
Пространственными называются размерные цепи, все или часть звеньев которых не параллельны друг другу и расположены в непараллельных плоскостях.
Угловыми называются размерные цепи, все звенья которых - угловые величины. Признаками составляющих размеров угловой цепи часто бывают отклонения от перпендикулярности, отклонения от параллельности осей и поверхностей и тому подобные погрешности взаимного расположения поверхностей и осей деталей.
Классификация звеньев размерных цепей
Таблица 1
| Определение | Примеры | |
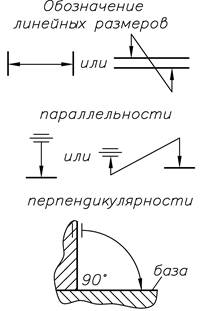
| Звено | Один из размеров, образующих размерную цепь. На схемах размерных цепей условно обозначают звенья: линейные размеры – двусторонней стрелкой; параллельность и перпендикулярность – односторонней стрелкой с направлением острия стрелки к базе |
|
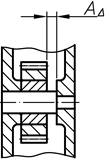
| Замыкающее | Звено размерной цепи, являющееся исходным при постановке задачи. Например, при конструировании, исходя из служебного назначения механизма, устанавливают технические требования (предельные размеры) к зазору А∆ - замыкающему звену |
|
| Звено размерной цепи, получающееся последним в результате решения поставленной задачи. Например, при сборке редуктора в его корпус 1 устанавливают зубчатое колесо 2 и вал 3. Последним звеном размерной цепи является зазор А∆ - замыкающее звено | 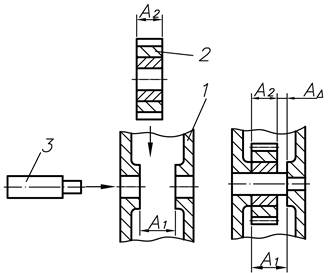
|
Продолжение табл. 1
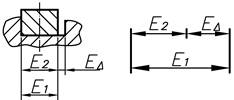
| Составляющее | Звено размерной цепи, функционально связанное с замыкающим звеном. Например, звенья Е1 и Е2 размерной цепи Е |
|
| Увеличивающее | Составляющее звено размерной цепи, с увеличением которого замыкающее звено увеличивается. Например, звено 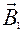 размерной цепи размерной цепи 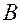
|
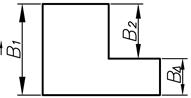
|
| Уменьшающее | Составляющее звено размерной цепи, с увеличением которого замыкающее звено уменьшается. Например, звено 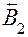 размерной цепи размерной цепи 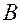
|
|
| Компенсирующее | Составляющее звено размерной цепи, изменением которого достигается требуемая точность замыкающего звена. Например, звено Ак – проставочное кольцо размерной цепи А | 
|
 |
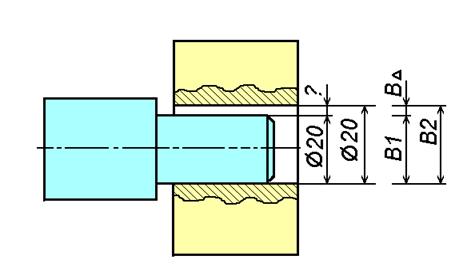 |
Рис. 2. Размерная цепь детали
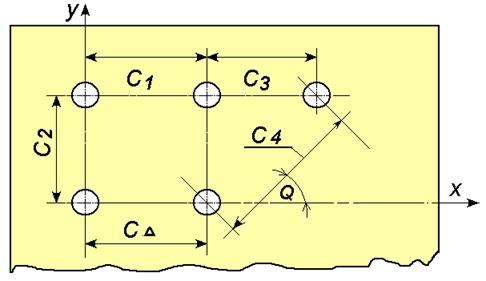 |
Рис. 3. Размерная цепь узла
Рис. 4. Плоскостная размерная цепь
В табл. 2 показана классификация размерных цепей.
Таблица 2
Виды размерных цепей
| Цепь | Определение |
| Технологическая | Размерная цепь, обеспечивающая требуемое расстояние или относительный поворот между поверхностями изготавливаемого изделия при выполнении операции или ряда операций сборки, обработки, при настройке станка или при расчете межпереходных размеров |
| Конструкторская | Размерная цепь, определяющая расстояние или относительный поворот между поверхностями или осями поверхностей деталей в изделии |
| Измерительная | Размерная цепь, возникающая при определении расстояния или относительного поворота между поверхностями, их осями или образующими поверхностями изготовляемого или изготовленного изделия |
| Линейная | Размерная цепь, звеньями которой являются линейные размеры |
| Угловая | Размерная цепь, звеньями которой являются угловые размеры |
| Плоская | Размерная цепь, звенья которой расположены в одной или нескольких параллельных плоскостях |
| Пространственная | Размерная цепь, звенья которой расположены в непараллельных плоскостях |
Увеличивающими называются составляющие размеры, при увеличении которых замыкающий размер увеличивается.
Уменьшающими называются составляющие размеры, при увеличении которых замыкающий размер уменьшается.
Например, достаточно добавить некоторую малую величину 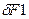 к размеру
к размеру 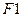 (см. рис. 4), при постоянстве остальных размеров цепи (здесь это только
(см. рис. 4), при постоянстве остальных размеров цепи (здесь это только 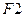 ), чтобы F∆ уменьшился. Если же, оставив неизменным
), чтобы F∆ уменьшился. Если же, оставив неизменным 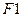 , добавить
, добавить 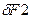 , то замыкающий F∆ увеличится.
, то замыкающий F∆ увеличится.
Учитывая разделение размеров на увеличивающие и уменьшающие не трудно записать уравнение размерной цепи в номиналах
АΔ = 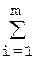 Ai ув –
Ai ув – 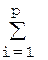 Ai ум (1)
Ai ум (1)
где в размерной цепи:
m - количество увеличивающих размеров,(Ai ув),
p - количество уменьшающих размеров (Ai ум).
Всего номинальных размеров составляющих звеньев, с учётом замыкающего, будет: n=m+ p+1
Предельные значения размеров замыкающего звена определяются по уравнениям, логически вытекающим из выражения (1) и определений увеличивающих и уменьшающих размеров:
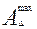 =
= 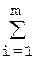
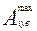 –
– 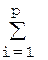
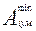 (2)
(2)
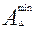 =
= 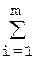
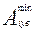 –
– 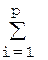
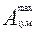 (3)
(3)
где: 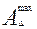 ,
, 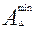 - наибольший и наименьший предельные размеры замыкающего звена;
- наибольший и наименьший предельные размеры замыкающего звена;
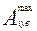 ,
, 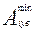 ,
, 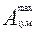 ,
, 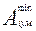 - наибольшие и наименьшие предельные размеры звеньев.
- наибольшие и наименьшие предельные размеры звеньев.
Допуск замыкающего размера вычисляется как разность наибольшего (2) и наименьшего (3) значений замыкающего, т. е. достаточно сложить два последних уравнения и получим
TAΔ = 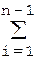 TAi (4)
TAi (4)
где: TAΔ -допуск замыкающего размера;
TAi - допуск составляющего размера;
n–1 - количество составляющих звеньев размерной цепи, без замыкающего.
В общем случае для размеров размерной цепи A справедливо соотношение:
TAΔ = 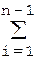 │
│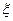 │ TAi(5)
│ TAi(5)
где: 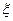 =
=
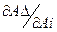 - передаточное отношение, n – число звеньев цепи.
- передаточное отношение, n – число звеньев цепи.
Если же проводится анализ цепей с параллельными звеньями, то:
для увеличивающих размеров 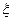 =+1,
=+1,
для уменьшающих размеров 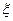 =- 1.
=- 1.
Параметр 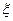 наиболее необходим при формализации решения задач, например при программировании.
наиболее необходим при формализации решения задач, например при программировании.
Предельные значения составляющих размеров и замыкающего звена в случае, если размеры заданы номинальными значениями и отклонениями, определяются по формулам:
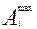 = Аi + ESi
= Аi + ESi
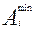 = Аi + EIi
= Аi + EIi
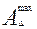 = АΔ + ESΔ (6)
= АΔ + ESΔ (6)
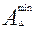 = АΔ + EIΔ, (7)
= АΔ + EIΔ, (7)
где: Аi, АΔ - номинальное значения составляющих и замыкающего размера,
ESi, EIi, ESΔ, EIΔ - верхнее и нижнее отклонения составляющих и замыкающего размера.
Воспользуемся уравнением
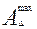 =
= 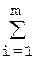
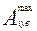 –
– 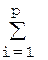
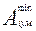
Запишем его с учётом рассмотренных выше определений предельных значений
АΔ + ESΔ = 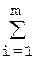 (Аiув + ESiув)–
(Аiув + ESiув)– 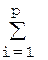 (Аiум + EIiум)
(Аiум + EIiум)
Подставим в левой части уравнения
АΔ = 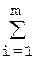 Ai ув –
Ai ув – 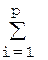 Ai ум
Ai ум
Верхнее и нижнее отклонения замыкающего размера в этом случае определяются по уравнениям размерной цепи в отклонениях:
ESΔ = 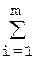 ESi ув –
ESi ув – 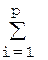 EIi ум (8)
EIi ум (8)
EIΔ = 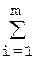 EIi ув –
EIi ув – 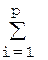 ESi ум, (9)
ESi ум, (9)
где: ESi ув, EIi ув, ESi ум, EIi ум - верхнее и нижнее отклонения увеличивающих и уменьшающих составляющих звеньев размерной цепи.
При решении ряда задач по размерному анализу верхнее и нижнее отклонения замыкающего размера удобнее определять по формулам через координату середины поля допуска:
ESΔ = Δ0 АΔ + 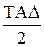 (10)
(10)
EIΔ = Δ0 АΔ – 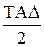 , (11)
, (11)
где: Δ0АΔ - TАΔ - допуск на замыкающее звено, определяемый по формуле (5).
Координата середины поля допуска замыкающего звена, определяется по уравнению середин полей допусков размерной цепи:
Δ0 АΔ = 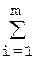 Δ0 Аi ув –
Δ0 Аi ув – 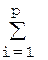 Δ0 Аi ум, (12)
Δ0 Аi ум, (12)
где: Δ0 Аi ув, Δ0 Аi ум - координаты середины поля допуска составляющих звеньев размерной цепи, определяемые по зависимости:
Δ0 Аi = (ESi + EIi)/2
С учётом выражений(11) и (12), верхнее и нижнее отклонения замыкающего размера определяются по формулам:
ESΔ = (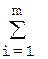 Δ0 Аi ув –
Δ0 Аi ув – 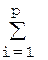 Δ0 Аi ум) +
Δ0 Аi ум) + 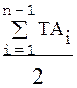 (13)
(13)
EIΔ = (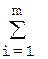 Δ0 Аi ув –
Δ0 Аi ув – 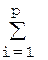 Δ0 Аi ум) –
Δ0 Аi ум) – 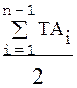 (14)
(14)
Известно, что величина допуска каждого составляющего размера определяется по формуле:
TAi = a i ∙ ii,
где: a - коэффициент точности; ii = 0.45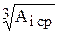 + 0.001Ai ср - единица допуска.
+ 0.001Ai ср - единица допуска.
Но следует полагать, что все составляющие звенья цепи одного уровня точности, что позволяет записать:
a 1 = a 2 = a 3 = a 4 =…= a n-1 = a = const
Тогда:
TAi = a (0.45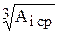 + 0.001Ai ср),
+ 0.001Ai ср),
Ai ср - средний размер интервала размеров.
Учитывая уравнение (5) ТАΔ = 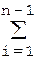 TAi,
TAi,
Или
ТАΔ = a ∙ i1 + a ∙ i2 + … a ∙ in-1= a∙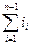
теперь можно записать:
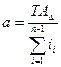
Если же изначально в размерной цепи некоторые размеры были с заданными допусками (например, размеры подшипников и т.д.), то уравнение (5) примет вид:
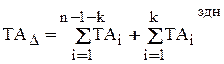 .
.
Здесь к – число размеров с заданными допусками. Теперь окончательно уравнение для коэффициента точности будет:
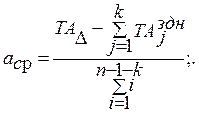 (15)
(15)
Определив коэффициент точности, можно вычислить допуски как TAi = а·ii, но рациональнее по таблице допусков выбирать допуски по ближайшему квалитету. В случае одинаковых размеров составляющих звеньев или же размеров находящихся в стандартном интервале размеров, где «i» неизменно для интервала, формула упрощается
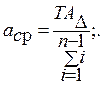 или TАi = ТА∆/(n-1) (16)
или TАi = ТА∆/(n-1) (16)
Как видно получен единый допуск для всех размеров. Способ этот прост, но по сути ориентировочный и поэтому применяется, в основном, лишь для предварительного назначения допусков составляющих размеров.
Допуски для размеров назначают, как для основного вала и основного отверстия, т.е. для увеличивающих в «+» а уменьшающих в «-», за исключением увязочного. Для увязочного размера положение допуска определяется по одному из уравнений, связывающих параметры замыкающего размера и составляющих, при назначенных параметров остальных.
Приведённые зависимости справедливы для метода полной взаимозаменяемости (МПВ), где предполагается равновероятное распределение получаемых размеров. Иначе говоря, при стрельбе в круглую мишень с прицеливанием в середину мишени, вероятность попадания в «1» и в «10» одинакова, что не совсем верно.
Теоретико-вероятностный метод (ТВМ)
Теоретико-вероятностный метод (ТВМ) основывается на вероятностных кривых распределения и как результат применяет несколько отличные формулы (здесь приводим без вывода). В представленных зависимостях предусмотрено равновероятностное распределение и коэффициент риска 0.27%.
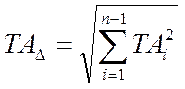 …………………………(17)
…………………………(17)
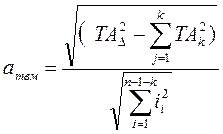 …………………………(18)
…………………………(18)
Значение допуска увязочного размера в ТВМ определяется по зависимости
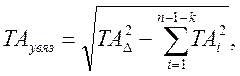 …………………………(19)
…………………………(19)
Из формул не трудно заметить, что для ТВМ допуски будут шире, чем для МПВ
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2756; Нарушение авторских прав?; Мы поможем в написании вашей работы!