Случайная величина. Закон распределения

Лекция 4 Случайные величины и их описание

Источники

1.Кроль В.М. Психология и педагогика / учебное пособие. – М, 2006 г.

Интернет-ресурсы по курсу «Психология и педагогика»

psychology-online.net - сайт "Научная и популярная психология" Библиотека. Мастерская (Компьютерная психодиагностика, Психологический практикум). Психоскоп. Путеводитель (ссылки). Exam Online (6 тестов).

● flogiston.ru - сайт " Флогистон. Психология из первых рук. " Библиотека. (Тематические подборки статей.)

● ido.rudn.ru (Психология и Педагогика) - электронный учебник по курсу "Психология и Педагогика" (авт.: Богданов И.В., Лазарев С.В. и др.) от Федерального фонда учебных курсов на портале Института Дистанц. Образования.

Пусть некоторая величина X в ряде испытаний может принимать различные числовые значения. Если значение величины Х в каждом данном испытании не может быть указано заранее (непред­сказуемо), то величина Х называется случайной величиной. Другими словами случайной называют величину, которая в результате опыта (наблюдения, измерения) принимает одно возможное, но заранее неизвестное значение. Случайная величина может быть дискретной или непрерывной.

Если случайная величина может принимать бесконечное множе­ство значений, причем эти значения могут быть сколь угодно близ­ки друг к другу, то такая величина называется непрерывной случай­ной величиной. Если же случайная величина может принимать лишь дискретные значения, то она называ­ется дискретной случайной величиной.

Примеры непрерывной случайной величины: сопротивление резистора (экземпляра) из партии со значением R = 1 кОм ± 10%; коэффициент усиления β транзистора (экземпляра), для которого по техническим условиям β ≥ 20.

Примеры дискретных случайных величин: число отказов электронного устройства (ЭУ) за рассматриваемый календарный период времени, например два года (возможные значения 0, 1, 2, 3, 4, …); частота попадания сопротивления резистора, взятого из партии с сопротивлением R = 1 кОм ± 10%, в диапазон (950…1000 Ом) при десяти наблюдениях (возможные значения 0, 1/10, 2/10, 3/10, …, 9/10, 1).

Охарактеризовать случайную величину можно при помощи закона распределения.

Под законом распределения случайной величины понимается со­ответствие, устанавливающее связь между возможными значениями случайной величины и вероятностями принятия этих значений. Это соответствие может быть задано в виде таблицы, графика или мате­матической формулы.

Ряд распределения. Под рядом распределения понимают таблицу вида, показанного на рис.4.1. Здесь случайная величина n – число отказов ЭУ за два года эксплуатации; p (n) – вероятность значения n.

n						…
p (n)	0,1	0,25	0,3	0,15	0,1	…

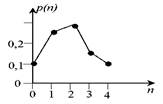
Рисунок 4.1 – Ряд распределения

Многоугольник распределения. Под многоугольником распределения понимают фигуру, изображённую на рис.4.2 (для случайной величины n, рассмотренной в предыдущем вопросе).

Рисунок 4.2 - Многоугольник распределения  

Функция распределения. Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения. Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения Х в i -м опыте окажется меньшим некоторого текущего значения х_i, от самой величины х. Другими словами под функцией распределения случайной величины Х для текущего значения х понимают вероятность не события Х = х, а вероятность события Х < х. Обозначают это как F (x) = P (X < x). На рис.4.3 показаны примеры функций распределения вероятности.

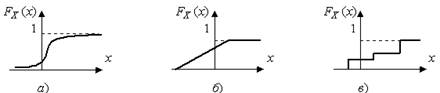
Рисунок 4.3 – Интегральные функции распределения

Свойства функции F (х):

1. F (х) – неубывающая функция, т.е. F (х ₂) ≥ F (х ₁) при х ₂ > х ₁.

2. F (х = – ∞) = 0.

3. F (х = + ∞) = 1

Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей, свойства которой будут рассмотрены ниже

Дата добавления: 2014-01-20