Модули шаровой и девиаторный упругости

Коэффициенты 3 К и 2 G в формулах (5.17) и в других случаях несколько неудобны из-за наличия в них цифровых множителей. Введем более естественное их обозначение, одной буквой:

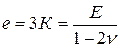, . (5.18)

Физический смысл их выявляется из нижеследующих выкладок. Например, закон Гука для объемной деформации в прямой и обратной форме, соответственно, теперь примет вид:

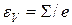и 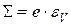. (5.19)

Смысл коэффициента e в формулах (12.16) стал очевиден: он характеризует сопротивляемость материала упругого тела его объемной деформации и может быть назван «модулем объемной деформации».

Кроме того, если использовать понятия средних напряжений и деформаций, определяемых формулам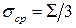и и , то второе выражения (5.19) примет вид

. (5.20)

Закон Гука при этом утверждает, что среднее нормальное напряжение пропорционально средней линейной деформации. В такой записи коэффициент е может быть назван «модулем средних линейных деформаций».

Обобщенный смысл коэффициента е выявляется из закона Гука, устанавливающего связь шаровых тензоров напряжений и деформаций. Эта связь может быть представлена в свернутом виде

(5.21)

или в развернутом:

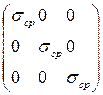= . (5.22)

Следовательно, коэффициент , равный отношению 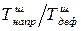двух шаровых тензоров, можно назвать модулем шаровых тензоров (напряжений и деформаций) или шаровым модулем упругости.

Удобство коэффициента g = 2 μ более четко проявится при установлении зависимостей между компонентами давиаторов напряжений и деформаций. С этой целью выпишем первое из уравнений:

. (a)

Постоянную Ламе (12.3) также выразим через g:

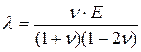
. (b)

Подстановка (b) в (a) дает:

. (c)

Выразим через тот же модуль и выражение (5.20) для среднего напряжения

. (d)

Теперь вычтем (d) из (c) и, с учетом того, что , найдем:

.

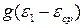Если выполним преобразования, аналогичные выкладкам (a) — (d), со вторым и третьим уравнением системы (12.4), то в результате она примет вид

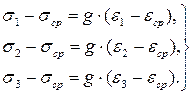(5.23)

Систему данных трех уравнений можно представить одним выражением:

= g× . (5.24)

Левую часть выражения (5.24) назовем девиатором напряжений, обозначив как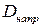, а правую часть — девиатором деформаций, обозначим как. Тогда закон упругости, представленный выражениями (5.23), или (5.24), можно записать в свернутом виде

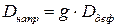. (5.25)

Следовательно, коэффициент , равный отношению девиатора напряжений к девиатору деформаций, нужно называть модулем девиаторных тензоров или девиаторным модулем сдвига.

Каждое из выражений, (5.25) или (5.25), эквивалентно системе трех уравнений (5.24) и выражает собой закон Гука для девиаторов, как закон изменения углов (закон искажения формы) элементарной частицы тела. При этом объемной деформации нет, она для девиатора всегда равна нулю:

.

Таким образом, компоненты напряжений и деформаций, соответствующие деформациям искажения формы элементарной частицы тела, пропорциональны друг другу. Дополнительно заметим, что девиаторный модуль g, в отличие от обычного модуля сдвига G можно еще назвать модулемпространственного (не плоского) сдвига.

Дата добавления: 2014-01-20