Закон Гука в условиях плоской задачи

Двухосное растяжение при плоском напряженном состоянии задается напряжениями σ ₁ > σ ₂ > σ ₃ = 0. При этом уравнения (5.1) примут вид:

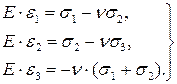(5.26)

Отсюда следует, что плоское напряженное состояние не исключает деформаций в третьем направлении. Например, пластинка, при ее двухосном растяжении, становится тоньше, чему отвечает знак минус последнего выражения.

Обратную форму закона Гука получим из (5.26), разрешив эту систему уравнений относительно напряжений:

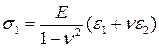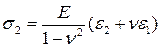, . (5.27)

Последние формулы широко используются для вычисления напряжений по экспериментально замеренным деформациям.

Двухосное сжатиезадается напряжениями σ ₃ < σ ₂ < σ ₁ = 0. При этом уравнения закона Гука выразятся через главные напряжения σ ₂ и σ ₃ и примут вид, аналогичный (5.26) и (5.27).

Состоянием чистого сдвига часто называют такой случай смешанного плоского напряженного состояния(σ ₁ > 0, σ ₂ = 0, σ ₃ < 0), при котором главные растягивающие и сжимающие напряжения равны по величине; например, когда σ ₁ = – σ ₃ = σ > 0. Уравнения (5.1) при этом упростятся и примут вид

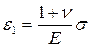, ε₂ = 0, 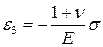(5.28)

или, то же самое,

ε ₁ = σ / g, ε₂ = 0, ε ₃ = – σ / g. (5.29)

В то же время оказывается, что здесь мы имеем случай и другой плоской задачи. Из (5.29), непосредственно, следует, что эти формулы удовлетворяют также смешанному плоскому деформированному состоянию, так как ε ₁ > 0, ε₂ = 0, ε ₃ < 0. Это состояние, при котором главные деформации ε ₁ и ε ₃ , также как и напряжения, равны по величине и противоположны по знаку, ε ₁ = – ε ₃ = σ / g.

Отсюда следует более строгая формулировка понятия «чистого сдвига», как такого особого состояния частицы материала упругого тела, при которомдва разных плоских состояния, напряженное и деформированное, тождественно совпадают.Диалектика понятия такова. Имеются два плоских состояния частицы тела: напряженное и деформированное (тезис и антитезис). Спрашивается: есть ли что общее между ними? Если есть, то это должно быть таким пограничным состоянием, в которой заданные два состояния сольются в неразличимом тождестве. Это и есть состояние чистого сдвига (синтез), которое в равной мере можно отнести как к плоскому напряженному состоянию, так и к состоянию плоской деформации.

Продолжим анализ формул (5.29). С этой целью, вычитая третье равенство из первой формулы системы, получим

σ = g× (ε ₁ – ε ₃) / 2. (a)

А так как g = 2 G, 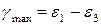и

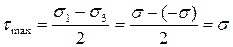, (b)

то выражение (a), учетом (b), примет вид закона Гука для чистого сдвига:

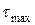= G× 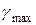. (5.30)

Выражение (5.30), получено из (5.29), как частного случая обобщенного закона Гука (5.1), который, в свою очередь, постулировался исходя из опытов на растяжение. Поэтому закон Гука при сдвиге, записанный в форме (5.30), можно рассматривать как следствие уже принятой пропорциональности между главными напряжениями и главными деформациями.

14 Ламе Габриель (1795 –– 1870) –– французский математик и инженер. В 1820 – 32 работал в Институте корпуса инженеров путейсообщения в Петербурге. Ввел (1859) коэффициенты Ламе и специальный класс функций, функции Ламе

Дата добавления: 2014-01-20