Время, ч

N dt

Обобщенная логистическая популяция

К настоящему времени существует много самых разных популяционных моделей с различными законами локального роста. Если, например, предположить, что коэффициенты рождаемости В и смертности D в (1.1) могут зависеть от N, считая по-прежнему, что от пространственных координат В и D не зависят, то уравнение (1.1) в силу (1.2) запишется следующим образом:

1. dN ₌ B – D,

N dt (1.5)

где В и D – функции рождаемости и смертности, зависящие от N.

Для многих видов функция рождаемости В определяется лишь физиологическими пределами рождаемости и не зависят от N, так что В (N) = n = С (С=const), где n – это так называемая естественная рождаемость (или плодовитость).

Что касается зависимости функции смертности D от N, то практически для всех популяций D(N) – монотонно возрастающая функция, причем D(0)=m > 0, где m – естественная смертность, а возрастание смертности с ростом N объясняется ростом конкуренции за определенный ресурс (питание, пространство и т.п.).

Рассмотрим более подробно этот тип популяции. Наиболее простая форма зависимости D(N) – линейная: D(N) = m + γN. Тогда

1. dN ₌ (m-n) – γN,

откуда

1. dN ₌ ε – γN,

N dt (1.6)

где ε = m – n – удельная скорость роста в отсутствии лимитирования, γ – коэффициент лимитирования, соответствующий потребности популяции к пище и называемой иногда «коэффициентом прожорливости»; слагаемое – γN в правой части уравнения (1.6) называют фактором тесноты. Это уравнение обычно записывают в виде

dN ₌ εN ﴾1 – γ N﴿

dt ε (1.7)

и называют логистическим уравнением или логистической моделью. Интегрируя логистическое уравнение, получим

ε N₀______

N = γ N₀ + (ε - N₀) e ^{- εt} (1.8)

γ

Популяция с таким законом роста называется логистической.

Отметим некоторые свойства решения (1.8). Во-первых из него следует, что

ε

Lim N(t)=γ

N

ε/γ < N₀

ε/γ > N₀

N₀

ε/γ < N₀

t

O

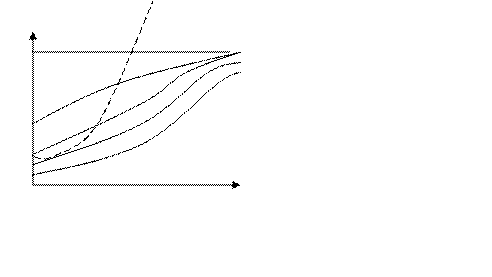
Рисунок 1 - Кривые изменения численности логистической популяции

т.е.численность популяции стремится к постоянной величине, которая прямо пропорциональна удельной скорости роста популяций нелимитированной среде ε и обратно пропорциональна коэффициенту лимитирования. При этом возможны два случая ε/γ > N₀; ε/γ < N₀.

Различие между этими случаями хорошо видно из рисунка 1. Отметим, что соотношение (1.8) описывает, в частности, популяции фруктовых вредителей и некоторых видов бактерий. Рост биомассы дрожжевых клеток в культуре и кривая роста, предсказанная логистическим уравнением, показаны на рисунке 2.

Биомасса дрожжей

450

Дата добавления: 2014-01-20