Определение напряжений в наклонных сечениях при растяжении (сжатии) в двух направлениях

А. б.

Рис. 18. Напряжения в наклонном сечении при растяжении (сжатии) в одном направлении

Определим напряжения, возникающие в наклонном сечении ВС, нормаль к которому повернута на угол α к направлению σ ₁. Обозначим S – площадь поперечного сечения стержня, а S_α – площадь наклонного сечения ВС. Тогда (1). В общем случае в наклонном сечении могут возникать σ_α и τ_α. Их значения найдем из условия равновесия отсеченной нижней части. Проецируем все силы на направление σ_α:

Σ Ρi = 0. Если 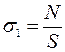, то N = σ · S, тогда 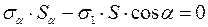(2). Подставив формулу (1) в формулу (2), получим

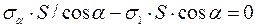, следовательно 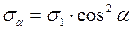(3).

Далее проецируем все силы на направление τ _α:

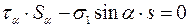(4).

Подставив формулу (1) в формулу (4), получим:

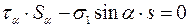, следовательно (5).

Выводы:

1. - наибольшее нормальное напрежение возникает в поперечном сечении бруса;

2. - наибольшее τ возникает на площадке, наклонённой под углом 45˚ к оси бруса и равно половине нормального напряжения, возникающего в соответствующей точке поперечного сечения;

3. Из формулы (5) 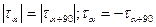- з акон парности касательных напряжений: касательные напряжения, возникающие на двух взаимно перпендикулярных пло-щадках равны по величине и противоположны по знаку, направлены к ребру пересечения площадок, либо от него (Рис. 21).

Рассмотрим случай плоского (двуосного) напряженного состояния, когда σ ₁ ≠ 0, σ ₂ ≠ 0. Мы уже знаем, что индексы стоят таким образом, что выполняется неравенство σ ₁ ≥ σ ₂. Положительный угол α между направлением σ ₁ и нормалью к произвольной площадке ВС отсчитываем против часовой стрелки. Между направлением напряжения σ₂ и наклонной площадкой ВС угол равен α + π/ 2 (Рис. 19а). Определим σ_α (суммируем напряжения на наклонной площадке от действия σ₁ с напряжениями от σ₂) и τ_α (суммируем напряжения от действия τ₁ с напряжениями от действия τ₂) (Рис. 19б).

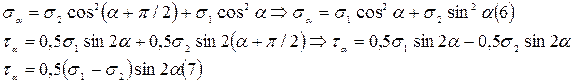
σ_α

τ_α

а. n α σ₁ С б. С

σ₂ α + π/ 2 σ_α τ_α

σ₂ σ₂

В σ₁ В σ₁

Рис. 19. Напряжения в наклонном сечении при растяжении (сжатии) в двух направлениях

Из формулы (7) следует, что τ_max = (σ₁ – σ₂) / 2 и имеют место в сечениях, наклоненных к σ₁ и σ₂ под одним и тем же углом α = 45˚, т.к. (sin 2 α = sin 90º =1). Для двухосного напряженного состояния также соблюдается закон парности касательных напряжений (Рис. 21).

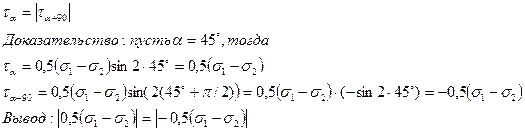
Рассмотрим частные случаи:

1. Предположим, что σ₁ = σ₂ = σ. Определим σ_α и τ _α.

В этом случае: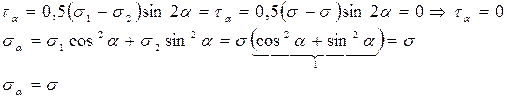

Если σ₁ = σ₂ = - σ, то σ_α = - σ. Такое напряженное состояние называют равномерным двуосным растяжением (Рис. 20а) или сжатием (Рис. 20б).

σ₁ =+ σ σ₁ = - σ

σ₂ = σ σ₂ = - σ

а. σ_α = + σ б. σ_α = - σ

Рис. 20. Двухосное растяжение и сжатие

2. Предположим также, что σ₁ = σ; σ₂ = 0; σ₃ = - σ (или σ₃ = + σ). Определим напряжения в сечениях наклонных к σ₁ под углом α = 45˚, а к σ₃ под углом α = 45º+ π /2 = 135º. Тогда для σ_α и τ _α получим:

Из формулы (6)

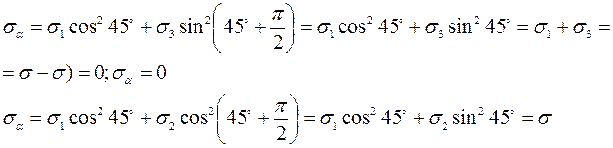
Такое напряженное состояние называют чистым сдвигом (Рис. 21).

σ₁ = σ

τ_α τ_α

σ₃ = - σ

τ_α

τ_α = ± σ

Рис.21. Чистый сдвиг и закон парности касательных напряжений

Дата добавления: 2014-01-11