Основные понятия. Числовые ряды. Основные понятия

Числовые ряды. Основные понятия. Необходимый признак сходимости ряда

РЯДЫ

Лекция18

Пусть задана некоторая бесконечная последовательность чисел:

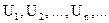
выражение

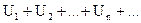
называется бесконечным числовым рядом (или просто рядом).

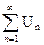
Числа 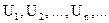– называются членами ряда, а член ряда – его общим членом.

Примеры рядов:

1)

2)

3)

Ряд можно задать с помощью общего члена, например, определяет следующий ряд:

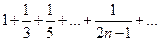
Частичной суммой 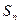числового ряда называетсясуммаего первых n членов,

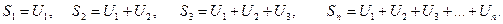
Суммой числового ряда S называется предел последовательности его частичных сумм, если этот предел существует

,

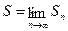причем ряд называется сходящимся, в противном случае, если же не существует, или то ряд называется расходящимся.

Пример 31 Исследовать на сходимость ряды

а)

б)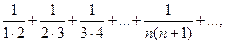

Решение:

а) Рассмотрим ряд . Найдем его частичные суммы Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.

б) Рассмотрим ряд

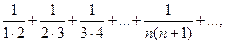
найдем его частичные суммы:

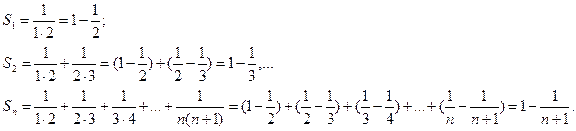
Так как то рассматриваемый ряд сходится: его сумма равна 1.

Пример 32 Исследовать на сходимость

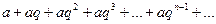
Решение:

Данный ряд составлен из членов геометрической прогрессии с первым членом 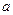и знаменателем (будем считать ):

,

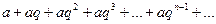известно, что сумма 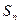первых n членов геометрической прогрессии определяется по формуле

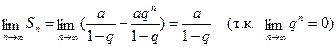Найдем , очевидно, что при , ряд сходится и его сумма 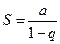. В остальных случаях, при , ряд расходится (доказать самостоятельно).

Например, ряд 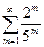сходится, т.к. q= и его сумма 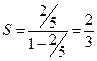, а ряд расходится, т.к. q=.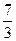

Дата добавления: 2014-01-11