
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементарные свойства сферической поверхности Земли
|
|
|
|
В первом приближении за фигуру Земли принимается шар с радиусом R =6400 км. В пределах территории 200´200 км с достаточной степенью приближения под фигурой Земли можно понимать шар с радиусом, равным среднему радиусу кривизны эллипсоида в центральной точке этой зоны.
Для решения ряда практических задач необходимо знать, в каких пределах расстояния, измеренные на сфере, можно заменить плоскими расстояниями, сферические углы в многоугольниках - плоскими углами и как влияет кривизна Земли на измеряемые превышения между точками (вертикальные расстояния).
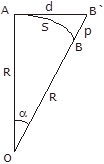
Рисунок 2 сферическое и плоское расстояние, понижение горизонта
При определении предела сферического расстояния S, рассматриваемого как плоское d (Рисунок 2), ставится условие, чтобы относительная разность S и d отвечала неравенству
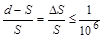 . (1)
. (1)
Такое условие ставится потому, что самые точные линейные измерения на местности выполняются именно с такой точностью.
На рисунке 2: S=AB – сферическое расстояние; d=AB¢ - плоское расстояние; R – радиус Земли, равный 6400 км; ar – центральный угол a, выраженный в радианной мере.
Из рисунка следует, что
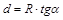 ;
; 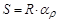 ;
;
 . (2)
. (2)
Выразив  в виде бесконечного ряда, получим
в виде бесконечного ряда, получим

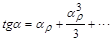 .
.
После подстановки этого выражения в (2) имеем
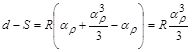 , (3)
, (3)
а так как  , то
, то
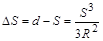 и
и  . (4)
. (4)
Учитывая поставленное условие (1), из решения неравенства находим, что
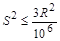 или
или 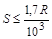 . (5)
. (5)
Подставив в последнее выражение значение среднего радиуса Земли R@ 6400 км, находим, что S £10,9 км. А распространяя аналогичные рассуждения и по другую сторону от точки A (см. Рисунок 2), приходим к выводу, что в пределах 22 км расстояния, измеряемые на сфере, практически равноценны плоским расстояниям.
Затем отметим, что в многоугольнике, построенном на сфере, сумма внутренних углов всегда больше суммы внутренних углов соответствующего плоского многоугольника на величину сферического избытка e. Для фигур земной поверхности с площадью P до нескольких сот квадратных километров сферический избыток e² можно вычислить по приближенной формуле
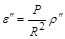 , (6)
, (6)
где  - значение радиана в секундах дуги;
- значение радиана в секундах дуги;  .
.
Например, для равностороннего прямоугольного треугольника со стороной S =20 км и P @200 км2 сферический избыток  . Поэтому при решении инженерно-геодезических задач на таких площадях можно считать, что сферические углы равны плоским углам.
. Поэтому при решении инженерно-геодезических задач на таких площадях можно считать, что сферические углы равны плоским углам.
Влияние кривизны Земли на измеряемые вертикальные расстояния (превышения) определяются величиной p понижения горизонта (Рисунок 2). Наблюдателю, расположенному в точке А, будет казаться, что точка В находится ниже горизонта на величину ВВ¢=p. При условии, что d << R, величину p вычисляют приближенно.
Из прямоугольного треугольника ОАВ¢ следует, что
 ;
;
или  ;
;
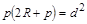 и
и 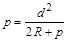 .
.
А так как в рассматриваемом случае p << R, то
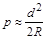 . (7)
. (7)
Для d =10 км p»8 м и пренебрегать влиянием кривизны Земли на измеряемые превышения нельзя.
При решении инженерно-геодезических задач поправку в измеренное превышение вводят, начиная с расстояния 100 м.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 3132; Нарушение авторских прав?; Мы поможем в написании вашей работы!