Принципы регистрации сигнала ЯМР

Блок-схема спектрометра ЯМР.

Классическая модель ЯМР.

Рассмотренная выше квантово-механическая модель описывает поведение отдельной частицы. Для описания поведения ансамбля (совокупности) частиц применяют классическую модель, впервые предложенную Блохом.

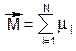Здесь практикуется понятие макроскопической (суммарной) ядерной намагниченности вещества. Ее вектор М представляет собой суму векторов m всех ядер:

Такая классическая модель соответствует квантово-механической. Поскольку на нижнем уровне больше частиц (m = + ½), ориентированных вдоль поля (их m_z ориентирован вдоль поля), то вектор ядерной намагниченности тоже ориентирован вдоль поля, при этом система магнитных ядер находится в тепловом равновесии (схемы А и В на следующей странице). Если систему коротким мощным импульсом электромагнитного излучения с частотой n_изл = n_прец вывести из равновесия путем быстрого увеличения числа магнитных ядер на верхнем уровне, а система не успеет на этот импульс отреагировать, то вектор М отклонится от равновесного положения на угол a,

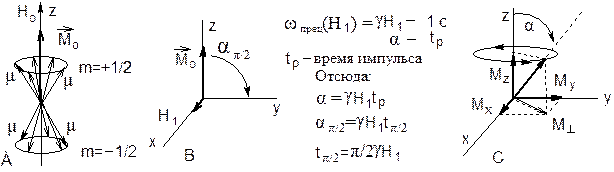
величина которого зависит от времени импульса (схема В). После выключения

импульса возвращение системы в равновесное состояние, называющееся релаксацией, зависит только от свойств самой системы. При этом вектор М одновременно начинает два движения – возвращение в исходное положение и прецессию вокруг силовых линий постоянного магнитного поля (см. схему С) с частотой, равной частоте прецессии отдельного магнитного момента ядра m, описанной в разделе 2.3. При этом скорости этих движений сильно отличаются. Если прецессия М совершается с частотой, равной рабочей частоте прибора (на современных приборах до 900 Мгц время оного вращения ~ 10^-9 с), тогда как время продольной релаксации (см. далее) ~ 3с.

Выведенный из равновесия вектор М (отклоненный на угол a, схема С) разложим на три компонента по декартовым координатам: М = М_x + M_y + M_z. Поперечный вектор М_^ определяется соотношением: М_^ = Ö М²_х + M²_y. Поскольку вектор М возвращается в равновесное состояние, то вектора М_x, M_y и M_z со временем изменяются.

Изменение продольного вектора M_z (продольная релаксация вдоль оси z) во времени t описывается дифференциальным уравнением первого порядка:

dM_z /dt = k₁(M_o – M_z), где k₁ = 1/ Т₁.

Константа скорости процесса k₁ имеет размерности обратного времени. Время Т₁ называют временем продольной или спин-решеточной релаксации. Решение дифференциального уравнения скорости:

· разделяем переменные: (dM_z)/(M_o – M_z) = k₁dt;

· вводим новую переменную: U=M_o-M_z, dM_z= - dU, - (dU)/U = k₁dt;

· интегрируем: - lnU = - ln(M_o-M_z) = k₁t + C;

· определяем постоянную интегрирования: t = 0, M_z = 0, C = - lnM_o;

·

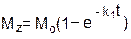конечное решение: ln[M_o/(M_o – M_z)] = k₁t или

Затухание поперечной компоненты М_^ описывается аналогичным дифференциальным уравнением:

- dM_^/dt = k₂М_^, где k₂ = 1/T₂.

Не всегда Т₂ = Т₁, в общем случае Т₂ ¹ Т₁. Тогда 1/ Т₂ = 1/T₁ + 1/T₂’, где

Т₁ – время продольной или спин-решеточной релаксации, Т₂ – время поперечной релаксации, T₂’ – время спин-спиновой релаксации. Решая это уравнение, находим:

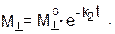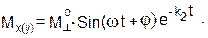При t = 0 М_^ = М_^°. Сами векторы М_х и М_у описываются функцией:

Здесь w - круговая частота прецессии, j - угол, учитывающий фазу: для М_х

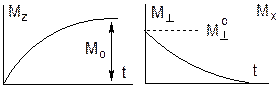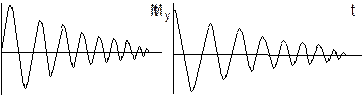j = 0, для М_у j = 90°. Изменение компонент M_z, M_^ , M_x и M_y­ показано на графиках:

D E F G

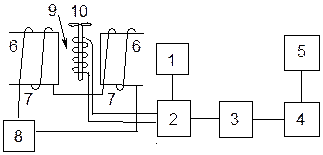Первый спектрометр Блоха с частотной разверткой спектра был двухкатушечным – одна электромагнитная катушка передавала на вещество излучение, другая – принимала. В дальнейшем с появлением импульсных методов наблюдения надобность в другой катушке отпала. Ниже представлена блок-схема однокатушечного прибора с полевой разверткой спектра:

Основные блоки: 1 – генератор радиоизлучения, 2 – радиочастотный мост, переключающий работу катушки с передачи на прием, 3 – усилитель, 4 – детектор, 5 – самописец, 6 – наконечники постоянного магнита, 7 – дополнительные, надетые на наконечники магнита электромагнитные катушки (соленоиды) и позволяющие изменять напряженность постоянного магнитного поля путем изменения силы постоянного тока в этих катушках, 8 – генератор развертки поля, питающий эти катушки, 9 – приемо-передающая катушка, 10 – ампула с веществом (стеклянная длинная и тонкая трубка с внутренним диаметром ~ 3 мм) с насаженным на нее воздушным пропеллером.

Современные приборы ЯМР скомбинированы с ЭВМ, которая управляет работой прибора и обрабатывает результаты наблюдения.

На воздушный пропеллер на ампуле направляется струя воздуха, заставляющая вращаться ампулу вокруг ее собственной оси и тем самым уменьшать негативное влияние неоднородности постоянного магнитного поля. Для уменьшения веса магнита и увеличения однородности постоянного магнитного поля в пространство между магнитом и приемо-передающей катушкой в современных приборах помещают специальные шиммирующие катушки для настройки однородности поля.

Наблюдать ПМР на резонансных частотах выше 100 МГц можно только с использованием сверхпроводящих магнитов. Соленоид, изготовленный из сплавов ниобия, погружен в емкость с жидким гелием. Эта емкость в свою очередь помещена в надежный криостат с кожухом, заполненный жидким азотом. Шиммирующие и приемо-передающая катушки с вращающейся ампулой внутри находятся в теплом отверстии магнита, в котором сохраняется комнатная температура, хотя совсем рядом размещены емкости с жидким гелием, температура которого всего 4 К.

Существует 2 способа наблюдения сигнала ЯМР – стационарный и импульсный.

3.3.1.. Стационарный метод наблюдения.

3.3.1.1. Частотная развертка спектра при H_o=const, ν_o=ν_изл, где ν_o -

переменная величина, если ν_o £ 60 МГц.

Этот способ был реализован впервые Блохом

3.3.1.2. Полевая развертка спектра при ν_o=const (технически удобно стабилизировать частоту на кварцевых кристаллах), Н_о незначительно изменяется при помощи дополнительных катушек на наконечниках магнита, ν_o > 60 МГц.

3.3.2. Импульсный (современный) метод наблюдения сигнала ЯМР с применением Фурье преобразованием.

Современные спектрометры ЯМР предназначены для работы на разных ядрах, что достигается изменением диапазона генерируемых частот

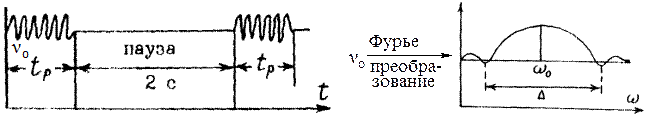
При импульсном методе на вещество воздействуют серией коротких импульсов продолжительностью ~ 10^-6 с, чередующихся с паузами в 2 с:

При этом монохроматическое излучение, по частоте близкое к частоте резонанса, при помощи Фурье преобразования превращается в полихроматическое с диапазоном D, перекрывающим частоты резонанса всех ядер по крайней мере одного элемента, благодаря чему все эти ядра возбуждаются (для них наступает резонанс).

Во время паузы система ядер возвращается в равновесное состояние и происходит излучение избытка энергии (спад свободной индукции – ССИ), что и улавливается приемной катушкой и многократно записывается в памяти ЭВМ, накапливаясь благодаря повторяющимся импульсам. Потом накопленный сигнал ССИ методом Фурье преобразуется в обычный, привычный для нас сигнал:

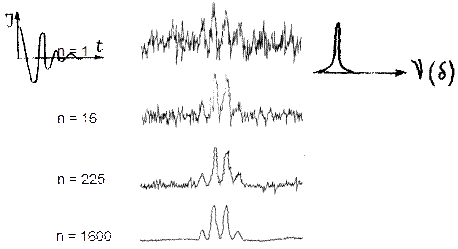За счет накопления большого количества импульсов возрастает соотношение сигнал/шум пропорционально Ön (n – число импульсов). Пример влияния накопления сигналов – метиленовый квартет в спектре 0,1 %-ного раствора этилбензола в ССl₄ в зависимости от числа n накопленных сигналов:

Преимущества импульсного метода:

А) Увеличение чувствительности метода.

Б) Исследование слабо резонирующих ядер, например ¹³С₆ (низькое

содержание в природе – 1 %, малая величина μ).

В) Изучение сразу всех магнитных ядер.

Дата добавления: 2014-01-20