Элементы и операции симметрии

При рассмотрении пространственного строения для описания такого строения необходимо привлечь такие геометрические понятия, как элементы симметрии, и операции симметрии, т.е. действия относительно этих элементов, приводящие к новой ориентации молекулы, неотличимой от исходной. Наиболее важными при этом являются такие элементы симметрии как ось, плоскость и центр симметрии. При этом можно провести такие операции симметрии как операция идентичности, вращение вокруг оси симметрии на определенный угол, отражение в плоскости симметрии и отражение в центре (т.е. в точке) симметрии.

10.6.1. Ось симметрии.

Если при вращении молекулы вокруг проходящей через нее оси на угол 360^о/n (это операция симметрии) она совмещается с первоначальной структурой n раз, то такая ось называется осью симметрии n-го порядка (С_n). Примеры:

Операция идентичности I (I = C₁) – поворот на 360⁰, т.е. вокруг оси 1-го порядка.

10.6.2. Плоскость симметрии или зеркальная плоскость.

Эта плоскость проходит через молекулу и делит ее на две симметричные части, т.е. одна часть, отражаясь в этой плоскости, дает вторую часть в стороне, противоположной от плоскости симметрии (по сути плоскость зеркала). В молекуле воды таких плоскостей две и обе они проходят через ось C₂ (символ вертикальной плоскости s_v): это плоскость молекулы, делящая все ее атомы пополам s_v(уz), и плоскость, перпендикулярная ей s_v(хz). В молекуле Cl-СН₃ таких плоскостей три, каждая из которых проходит через ось 3-го порядка и

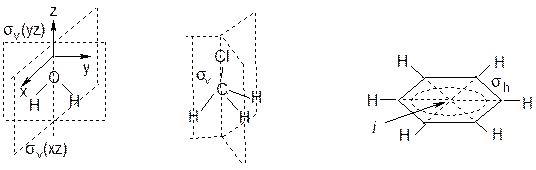одновременно через один из трех атомов водорода:

Молекула бензола еще более симметрична, она кроме оси шестого порядка, шести s_v, шести осей С₂, перпендикулярных оси s_v, имеет еще горизонтальную плоскость симметрии s_h и центр симметрии.

10.6.3. Центр симметрии.

В молекулах воды и хлористого метила центра симметрии нет, но он есть в молекуле бензола, это центр равностороннего шестиугольника. При наличии центра симметрии все атомы молекулы, не лежащие в центре симметрии, расположены попарно на одной прямой, проходящей через центр, на одинаковом расстоянии от центра, как, например, в бензоле (центр симметрии обозначается буквой i):

10.6.4. Зеркально-поворотная ось симметрии.

Этот элемент симметрии требует последовательного сочетания двух операций – поворот вокруг оси симметрии и отражения, например, зеркально-поворотная ось S₄:

10.6.5. Cвязь характера колебаний с их симметрией.

Теперь остается привязать движения атомов молекулы для нормальных колебаний к элементам симметрии (или к операциям симметрии) на примере молекул воды, относящихся к точечной группы С_2v.

Точечная группа симметрии – набор операций симметрии, которые можно применить к объекту, имеющему центр тяжести. Каждая точечная группа имеет свою таблицу характеров, которая для точечной группы С_2v имеет вид:

С2v	I C2(z) sv(xz) sv(yz)	движение
Неприводимые А1 Представления А2 Симметрии В1 В2	+1 +1 +1 +1 +1 +1 -1 -1 +1 -1 +1 -1 +1 -1 -1 +1	Вдоль z, n1, d Rz Вдоль x, Ry Вдоль y, Rx, n2

Здесь применяется символика для движения: R – вращение вокруг соответствующей оси координат, n - валентные и d - деформационные колебания. Символика симметрии колебаний представлена в следующей таблице:

Симметричные колебания	Антисимметричные Колебания	Относительно элемента симметрии
А A’ Аg А1	B A” Au A2	Главная ось симметрии С­n sh i sv

Другие используемые обозначения:

I - операция идентичности, т.е. превращение объекта самого в себя, что

идентично его вращению вокруг любой оси на 360 ^о;

Е - дважды вырожденные колебания, т.е. такие, которые раскладываются на

два взаимно перпендикулярные и имеющие одну и ту же частоту;

Т - трижды вырожденные колебания, т.е. такие, которые раскладываются на

три взаимно перпендикулярные и имеющие одну и ту же частоту;

В₁, В₂, В₃ – здесь индексы внизу не имеют никакого другого смысла, кроме

нумерации.

10.6.5.1. Симметричные колебания.

Если целая молекула, такая как Н₂О, или часть ее, например, группа >СН₂ или -NO₂, имеют два эквивалентных атома, то они имеют два разных по характеру симметрии колебания – симметричные и антисимметричные. Рассмотрим для примера колебание n₁ для молекулы воды, которое является симметричным, т.е. n₁ = n_s.

Симметричным называют такое колебательное движение, направление движения в котором после применения операции симметрии не изменяется.

Пример, колебание n₁:

Таким образом, колебание n₁ является полно симметричным и имеет характер симметрии А₁. Что же касается деформационного колебания, то его считают третьим: n₃ = d = n_s. То, что оно полно симметрично, доказывает применение операций симметрии:

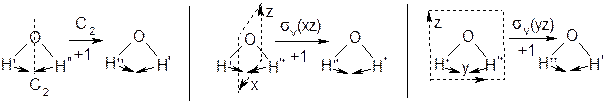10.6.5.2. Антисимметричные колебания.

Антисимметричным называют такое колебательное движение, направление движения в котором после применения операции симметрии изменяется на противоположное.

В качестве примера такого антисимметричного валентного колебания можно привести второе колебание молекулы воды: n₂ = n_as. Применение операций симметрии к этому колебанию показывает, что оно имеет характер симметрии В₂:

10.6.6. Методика отнесения молекул к определенным точечным группам.

Предлагается алгоритм отнесения молекул к определенным точечным группам начинать с операции симметрии С_¥, применяемой только к линейным молекулам (представлен на следующей странице). Там же представлены примеры молекул, относящиеся к различным точечным группам.

Дата добавления: 2014-01-20