Нормальное, тангенциальное и полное ускорения

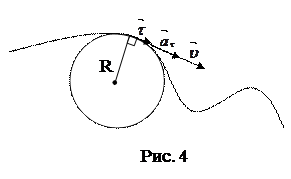
Движение тела характеризуется скоростью и ускорением, которые могут изменяться во времени. Пусть материальная точка движется по плоской криволинейной траектории с переменной по величине и направлению скоростью (рис. 4). Для характеристики степени криволинейности вводится понятие радиуса кривизны в данной точке траектории.

Радиусом кривизны R траектории называют радиус окружности, которая сливается с криволинейной траекторией на бесконечно малом ее участке.

В данной точке траектории касательная всегда перпендикулярна радиусу кривизны.

Пусть и скорость, и ускорение меняются по величине и направлению.

Мы знаем, что ускорение тела при движении есть .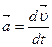

Вектор скорости можно представить как произведение модуля скорости и некоторого единичного вектора 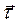, сонаправленного с вектором линейной скорости , направленного по касательной к траектории.

Таким образом, полное ускорение материальной точки при криволинейном движении можно представить в виде суммы двух слагаемых. Первое слагаемое .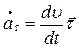

Вектор сонаправлен с вектором 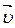, т.е. направлен по касательной к траектории и называется тангенциальным или касательным ускорением. Его модуль равен , поэтому 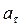характеризует быстроту изменения скорости криволинейного движения по величине, но не направлению, так как вектор не изменяется.

Следовательно, можно заключить, что - тангенциальное ускорение, характеризующее изменение скорости по величине, оно направлено по касательной к траектории.

Второе слагаемое называется нормальным ускорением. Что характеризует этот вектор, куда направлен, как его рассчитать?

Так как вектор 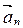сонаправлен с вектором , который определяет изменение направления вектора линейной скорости, то он характеризует изменение скорости криволинейного движения по направлению.

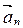Определим величину и направление . Рассмотрим частный случай движения материальной точки по окружности радиусом R с постоянной по величине скоростью (рис.5). Среднее изменение скорости на дуге АВ отнесем к точке С, лежащей посередине дуги.

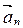направлено вдоль R к центру окружности.

∾:

.

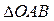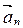перпендикулярно скорости, направлено вдоль радиуса к центру окружности. Его называют нормальным, радиальным или центростремительным ускорением.

Полное ускорение материальной точки при криволинейном движении характеризует быстроту изменения скорости как по величине, так и по направлению (рис.6).

, .

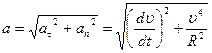Дата добавления: 2014-01-20