Тема №3: линеаризованные математические модели ОАС

Линеаризованные математические модели ОАС можно получить двумя способами:

Первый – исходя из законов сохранения, используя аналитическую линеаризацию нелинейных функциональных зависимостей, получают структуры моделей и, производя соответствующие расчёты по паспортным данным функциональных элементов, определяют параметры моделей.

Второй – исходя из экспериментальных характеристик (статических, временных и частотных), используя графическую линеаризацию, устанавливают структуру и вычисляют параметры моделей.

Математическая линеаризованная модель ИО+РМ была получена в лекции № 2. В форме линейного дифференциального уравнения с постоянными коэффициентами модель имеет такой вид:

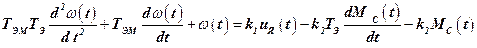, (1)

здесь 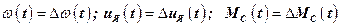; 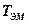– электромеханическая постоянная времени, 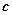; 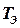– электромагнитная постоянная времени, 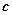; 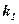– коэффициент передачи по управляющему – 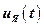воздействию, 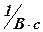; 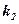– коэффициент передачи по возмущающему – 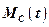воздействию, 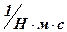; 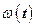– угловая скорость рабочего механизма, 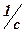; 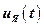– напряжение управления, подаваемое на якорную обмотку электродвигателя, 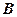; 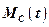– момент сопротивления рабочего механизма, .

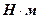Если в качестве характеристики момента сопротивления рабочего механизма использовать 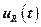, то уравнение (1) можно представить в таком виде

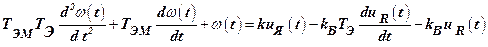, (2)

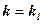здесь , а 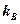– коэффициент передачи по возмущающему – 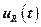воздействию, .

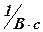Применив к обеим частям уравнения (2) преобразование Лапласа с использованием основных теорем операционного исчисления, получим

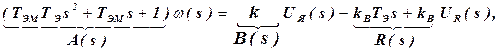, (3)

здесь 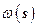– изображение выходного сигнала 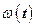; 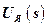– изображение управляющего воздействия 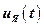; 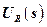– изображение возмущающего воздействия 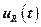; 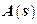, 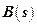и 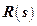– соответствующие полиномы комплексной переменной преобразований Лапласа .

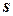Используя принцип суперпозиции (в чём его суть?) можем представить операторное уравнение (3) в форме следующих двух передаточных функций

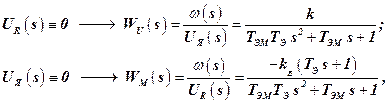(4)

где 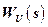– передаточная функция соединения ИО+РМ по управляющему воздействию; 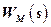– передаточная функция соединения ИО+РМ по возмущающему воздействию.

Изображение выходного сигнала 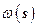с помощью передаточных функций можно представить так:

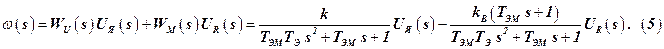
Новым функциональным элементом в ОАС является датчик – тахогенератор, преобразующий угловую скорость РМ в соответствующее изменение напряжения постоянного тока 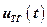. Тахогенератор представляет собой безинерционный функциональный элемент, статическая характеристика которого в рабочем диапазоне угловых скоростей аппроксимируется такой зависимостью

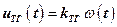, (6)

где 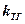– коэффициент передачи тахогенератора, 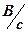. Применив преобразование Лапласа к уравнению (6), получим операторное уравнение вида

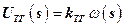, (7)

здесь 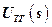– изображение напряжения тахогенератора 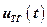; 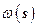– изображение угловой скорости 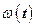. Тогда передаточная функция тахогенератора

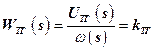. (8)

Теперь операторное уравнение ОАС представимо в таком виде

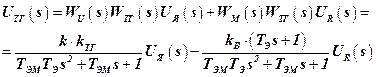. (9)

Исследуем функциональные особенности ОАС, включающего ИО+РМ+Д, с помощью линеаризованной модели (9). Определим переходные характеристики.

,

,

.

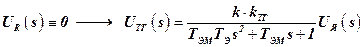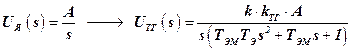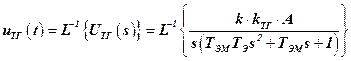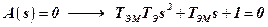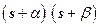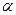Для действительных и различных корней характеристического уравнения , полином можно представить как , где и 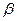– корни, тогда

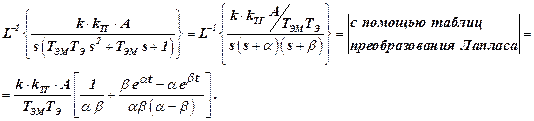
Итак,

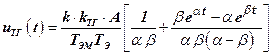. (10)

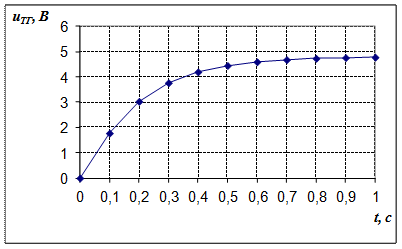
Пример 1. Построим график переходного процесса для ОАС, заданного передаточной функцией вида

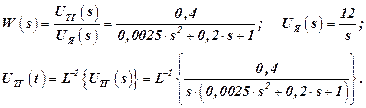
Определим корни характеристического уравнения

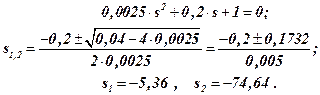
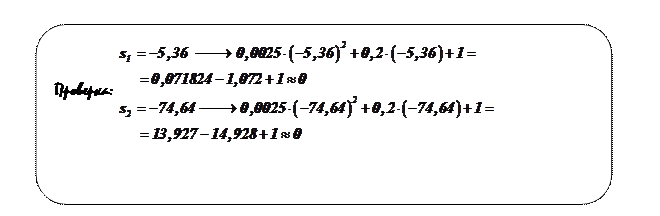
Подставив в выражение (10) получим

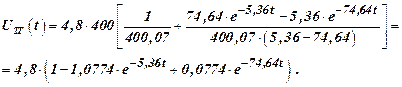
Проверка:

t, c	uТГ, B
	0,0000
0,1	1,7744
0,2	3,0297
0,3	3,7642
0,4	4,1940
0,5	4,4454
0,6	4,5925
0,7	4,6786
0,8	4,7290
0,9	4,7584
	4,7757

СОВЕТ КОНФУЦИЯ

:

Не делай другому того, чего себе не пожелаешь!

Дата добавления: 2014-01-20