Анализ изменения давления в цилиндре насоса в период всасывания

Рассмотрим процесс всасывания одноцилиндрового приводного насоса одинарного действия, который откачивает жидкость из приемного резервуара открытого типа. Давление на поверхности жидкости постоянно и равно р _о, ось цилиндра насоса, расположенного горизонтально, находится на высоте z _в от свободной поверхности перекачиваемой жидкости плотностью ρ.

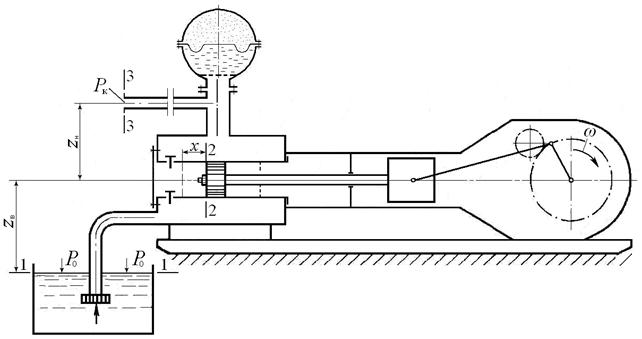
Рис. 10. Схема одноцилиндрового насоса одинарного действия.

Запишем уравнение Бернулли для двух сечений 1–1 и 2–2, приняв за плоскость сравнения сечение 1–1:

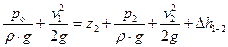, (18)

где v ₁ – скорость перемещения поверхности жидкости в сечении 1–1; z ₂= z _в – вертикальное расстояние между сечением 1–1 и центром тяжести сечения 2–2, совпадающего с поверхностью поршня, контактирующего с жидкостью; p ₂= p _ц – давление жидкости в цилиндре насоса в период всасывания; v ₂= v _п – скорость движения жидкости в цилиндре, равная скорости поршня; 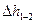– потери энергии на перемещение жидкости между рассматриваемыми сечениями.

При круговой циркуляции жидкости (характерной для ряда операций, выполняемых на скважинах) поверхность жидкости в приемном резервуаре практически неподвижна и v ₁=0.

Решая уравнение (18) относительно напора в цилиндре 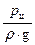с учетом высказанных замечаний, получим:

. (19)

Потери энергии между сечениями 1-1 и 2-2 состоят из потерь в местных сопротивлениях 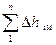всасывающего трубопровода, потерь по длине 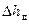и потерь на преодоление сил инерции в цилиндре 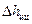и в трубопроводе:

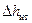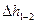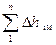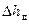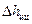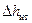=+++. (20)

Установлено, что потери в клапане изменяются особым образом в сравнении с другими местными сопротивлениями, поэтому выделим эти потери в виде отдельного слагаемого. Тогда местные потери представим в виде:

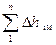=, (21)

где – потери напора во всасывающем клапане; 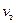– скорость движения жидкости во всасывающем трубопроводе; 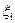– коэффициент местных потерь i -го местного сопротивления всасывающего трубопровода.

Выражая в уравнении (21) скорость движения жидкости в трубопроводе через скорость поршня, получим:

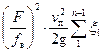=, (22)

где 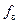– площадь поперечного сечения всасывающего трубопровода.

Потери напора по длине 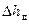всасывающего трубопровода (в уравнении 20) представим по известной формуле Дарси-Вейсбаха:

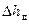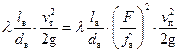=, (23)

где λ – коэффициент гидравлического трения; l _в – длина всасывающего трубопровода; d _в – внутренний диаметр всасывающего трубопровода.

С учетом отмеченных замечаний и обозначений, уравнение (19) примет вид:

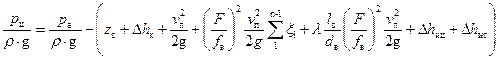. (24)

Объединим потери в местных сопротивлениях с потерями по длине:

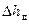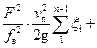
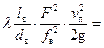
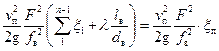+= , (25)

где 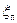– приведенный коэффициент гидравлических сопротивлений всасывающего трубопровода.

Подставив в уравнение (25) скорость движения поршня по уравнению (9), без учета влияния длины шатуна, получим:

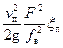
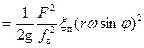. (26)

Потери напора на преодоление сил инерции жидкости в цилиндре вычислим по формуле:

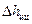
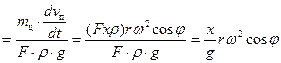, (27)

где m _ц – масса жидкости в цилиндре.

Аналогично вычислим потери напора на преодоление сил инерции жидкости в трубопроводе:

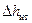
, (28)

где m _т – масса жидкости во всасывающем трубопроводе.

Для исключения из уравнений (26), (27) и (28) тригонометрических функций, воспользуемся уравнением (8) из которого выразим cos φ, а затем – sin φ:

cos φ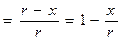. (29)

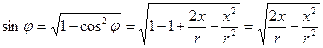. (30)

Подставив выражение (30) в уравнения (26), а (29)– в уравнения (27) и (28), получим:

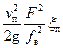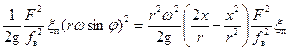=. (31)

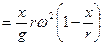. (32)

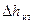
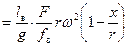. (33)

Кроме того, преобразуем в уравнении (24) выражение для скоростного напора к виду:

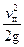
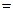
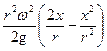. (34)

Подставив выражения (31) – (34) в уравнение (24) и выполнив некоторые преобразования, получим:

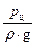
(35)

Умножив правую и левую части уравнения (35) на (ρ∙g) получим зависимость давления в цилиндре насоса от величины х перемещения поршня:

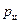
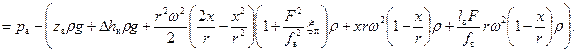(36)

Анализ уравнения (36) показывает, минимальное давление в цилиндре насоса будет в начале процесса всасывания (при х =0), а максимальное – в конце (при х =2 r). Тогда, уравнение (36) соответственно примет вид:

(37)

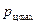
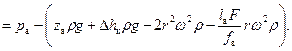(38)

Дата добавления: 2014-01-20