Построение модели множественной регрессии

Окончательно уравнение парной линейной регрессии, связывающая величину доли денежных доходов населения, направленных на прирост сбережений (у) с величиной среднемесячной начисленной заработной платы (х) имеет вид

С использованием F- критерия установлено, что полученное уравнение парной регрессии в целом является статистически значимым, и адекватно описывает изучаемое явление связи величины чистого дохода условной фирмы у с оборотом капитала х1и использованным капиталомх2.

Сформирована эконометрическая модель множественной линейной регрессии, связывающая величину чистого дохода условной фирмы у с оборотом капитала х1и использованным капиталомх2:.

С использованием F- критерия установлено, что полученное уравнение парной регрессии в целом является статистически незначимым, и не адекватно описывает изучаемое явление связи величины ежемесячной пенсии у с величиной прожиточного минимума х.

7. Путем расчета коэффициентов эластичности показано, что при изменении оборота капитала 1% величина чистого дохода копании изменяется на 0,0008%, а при изменении использованного капитала на 1% величина чистого дохода компании изменяется на 0,56%.

8. С использованием t – критерия выполнена оценка статистической значимость коэффициентов регрессии Установлено, что объясняющая переменная х₁ является статистически незначимой и ее можно исключить из уравнения регрессии в тоже время объясняющая переменная х₂ является статистически значимой.

10. Рассчитана средняя ошибка аппроксимации статистических данных линейным уравнением множественной регрессии, которая составила 29,8%. Показано, за счет какого наблюдения в статистической базе величина данной ошибки превышает допустимое значение.

Построение модели парной регрессии «вручную»

Используя статистический материал, приведенный в таблице 1.4 необходимо:

1. Рассчитать параметры уравнения линейной парной регрессии.

2. Оценить тесноту связи с помощью показателей корреляции и детерминации.

3. Используя коэффициент эластичности, определить степень связи факторного признака с результативным.

4. Определить среднюю ошибку аппроксимации.

5. Оценить с помощью F-критерия Фишера статистическую надежность моделирования.

Таблица 1.4. Исходные данные.

№ п.п	Область	Доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и на покупку валюты, в общей сумме среднедушевого денежного дохода, %,yi	Среднемесячная начисленная заработная плата, у.д.е.,xi
1.	Калужская	8,4
2.	Костромская	6,1
3.	Орловская	9,4
4.	Рязанская	11,0
5.	Смоленская	6,4
	ИТОГО:	41,3

Для определения неизвестных параметров b₀, b₁ уравнения парной линейной регрессии (1) используем стандартную систему нормальных уравнений, которая имеет вид

(1.9)

Для решения этой системы вначале необходимо определить значения величин Sх² и Sху. Эти значения определяем из таблицы исходных данных, дополняя ее соответствующими колонками (таблица 3.5)

Таблица 1.5. К расчету коэффициентов регрессии

№ п.п	yi	xi
1.	8,4			2881,2
2.	6,1			2171,6
3.	9,4			2716,6
4.	11,0			3751,0
5.	6,4			2092,8
S	41,3			13613,2

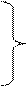Тогда система (3.1.9) приобретает вид

(1.10)

Выражая из первого уравнения b₀ и подставляя полученное выражение, во второе уравнение получим

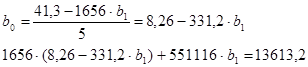
Производя почленное умножение и раскрывая скобки, получим

Откуда

Тогда

(1.11)

Далее, в соответствии с заданием необходимо оценить тесноту статистической связи зависимой переменной у с объясняющей переменной х с помощью показателей корреляции и детерминации.

Так, как построено уравнение парной линейной регрессии, то определяем линейный коэффициент корреляции по зависимости

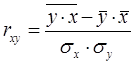, (1.12)

где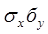- значения среднеквадратических отклонений соответствующих параметров.

Для расчета линейного коэффициента корреляции по зависимости (1.12) выполним промежуточные расчеты

Подставляя значения найденных параметров в выражение (1.12) получим

.

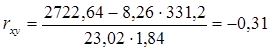Полученное значение линейного коэффициента корреляции свидетельствует о наличии слабой обратной статистической связи между величину доли денежных доходов населения, направленных на прирост сбережений (у) и величины среднемесячной начисленной заработной платы (х).

Коэффициент детерминации равен , что означает, что только 9,6% объясняется регрессией объясняющей переменной х на величину у. Соответственно величина 1- равная 90,4 % характеризует долю дисперсии переменной у, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных.

Коэффициент эластичности определяется по зависимости (3.1.3) и равен

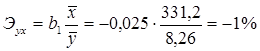
Следовательно, при изменении величины среднемесячной начисленной заработной платы на 1% величина доли денежных доходов населения, направленных на прирост сбережений также снижается на 1%, причем при увеличении заработной платы наблюдается снижение величины доли денежных доходов населения, направленных на прирост сбережений. Данный вывод противоречит здравому смыслу и может быть объяснен только некорректностью сформированной математической модели.

Для определения средней ошибки аппроксимации воспользуемся зависимостью (1.4). Для удобства расчетов преобразуем таблицу 1.4 к виду таблица 1.6 В данной таблице в колонке 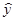рассчитаны текущие значения объясняющей переменной с использованием зависимости (1.9).

Таблица 1.6. К расчету средней ошибки аппроксимации

№ п./п	yi	xi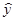
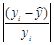
1.	8,4		8,0	0,048
2.	6,1		7,6	0,246
3.	9,4		9,3	0,011
4.	11,0		8,0	0,273
5.	6,4		8,4	0,313
S	41,3		41,3	0,89

Тогда средняя ошибка аппроксимации равна

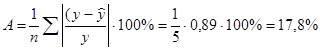
Полученное значение превышает (12…15)%, что свидетельствует о существенности среднего отклонения расчетных данных от фактических, по которым построена эконометрическая модель.

Надежность статистического моделирования выполним на основе F – критерия Фишера. Технология использования данного критерия приведена в п.п. 1.2.

Теоретическое значение критерия Фишера F_т определяется из соотношения значений факторной и остаточной 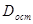дисперсий, рассчитанных на одну степень свободы по формуле

; (1.13)

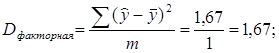
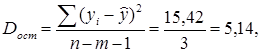
где n - число наблюдений; m - число объясняющих переменных (для рассматриваемого примера m =1).

Тогда

Критического значения F_крит, определяется по статистическим таблицам и для уровня значимости a = 0, 05 равняется 10,13. Так как F_Т < F_крит, то нулевая гипотеза не отвергается, и полученное уравнение регрессии принимается статистически незначимым.

Используя статистический материал, приведенный в таблице 1.7 необходимо:

1. Построить линейное уравнение множественной регрессии, пояснить экономический смысл его параметров.

2. Дать сравнительную оценку тесноты связи факторов с результативным признаком с помощью средних (общих) коэффициентов эластичности.

3. Оценить статистическую значимость коэффициентов регрессии с помощью t – критерия и нулевую гипотезу о не значимости уравнения с помощью F – критерия.

4. Оценить качество уравнения посредством определения средней ошибки аппроксимации.

Таблица 1.7. Исходные данные

№ п/п	Чистый доход, млн. долл.США	Оборот капитала млн. долл. США	Использованный капитал, млн. долл. США
yi	x1i	x2i
1.	1,50	5,90	5,90
2.	5,50	53,10	27,10
3.	2,40	18,80	11,20
4.	3,00	35,30	16,40
5.	4,20	71,90	32,50
6.	2,70	93,60	25,40
7.	1,60	10,00	6,40
8.	2,40	31,50	12,50
9.	3,30	36,70	14,30
10.	1,80	13,80	6,50
S	28,40	370,60	158,20

Для определения неизвестных параметров b₀, b₁, b₂ уравнения множественной линейной регрессии используем стандартную систему нормальных уравнений, которая имеет вид

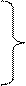
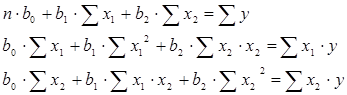(2.1)

Для решения этой системы вначале необходимо определить значения величин Sх₁², Sх₂², Sх₁у, Sх₂у, Sх₁х₂. Эти значения определяем из таблицы исходных данных, дополняя ее соответствующими колонками (таблица 3.8)

Таблица 2.8. К расчету коэффициентов регрессии

№ п.п	yi	x1i	x2i	x1iyi	x2iyi	x1ix2i
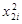
1.	1,50	5,90	5,90	8,85	8,85	34,81	34,81	34,81
2.	5,50	53,10	27,10	292,05	149,05	1439,01	2819,61	734,41
3.	2,40	18,80	11,20	45,12	26,88	210,56	353,44	125,44
4.	3,00	35,30	16,40	105,90	49,20	578,92	1246,09	268,96
5.	4,20	71,90	32,50	301,98	136,50	2336,75	5169,61	1056,25
6.	2,70	93,60	25,40	252,72	68,58	2377,44	8760,96	645,16
7.	1,60	10,00	6,40	16,00	10,24	64,00	100,00	40,96
8.	2,40	31,50	12,50	75,60	30,00	393,75	992,25	156,25
9.	3,30	36,70	14,30	121,11	47,19	524,81	1346,89	204,49
10.	1,80	13,80	6,50	24,84	11,70	89,70	190,44	42,25
S	28,40	370,60	158,20	1244,17	538,19	8049,75	21014,10	3308,98

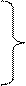Тогда система (3.1.14) приобретает вид

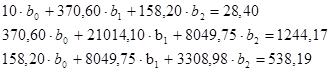(2.2)

Для решения данной системы воспользуемся методом Гаусса, который заключается в последовательном исключении неизвестных: делим первое уравнение системы на 10, затем умножаем полученное уравнение на 370,6 и вычитаем его из второго уравнения системы, далее умножаем полученное уравнение на 158,20 и вычитаем его из третьего уравнения системы. Повторяя указанный алгоритм для преобразованных второго и третьего уравнений системы получим

ÞÞ

Þ.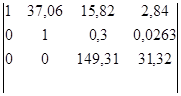

После преобразования имеем

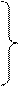
(2.3)

Откуда

.

.

Тогда окончательно зависимость чистого дохода от оборота капитала и использованного капитала в виде линейного уравнения множественной регрессии имеет вид

(2.4)

Из полученного эконометрического уравнения видно, что с увеличением используемого капитала чистый доход увеличивается и наоборот с увеличением оборота капитала, чистый доход уменьшается. Кроме того, чем больше величина коэффициента регрессии, тем значительнее влияние объясняющей переменной на зависимую переменную. В рассматриваемом примере величина коэффициента регрессии больше чем величина коэффициента, 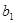следовательно, используемый капитал оказывает значительно большее влияние на чистый доход, чем оборот капитала. Для количественной оценки указанного вывода определим частные коэффициенты эластичности.

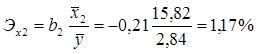
Анализ полученных результатов так же показывает, что большее влияние на чистый доход оказывает используемый капитал. Так в частности, при увеличении используемого капитала на 1% чистый доход увеличивается на 1,17%. В то же время с ростом оборота капитала на 1%, чистый доход снижается на 0,5%.

Теоретическое значение критерия Фишера F_т

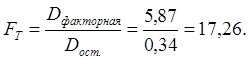(2.5)

где

Величина критического значения F_крит, определяется по статистическим таблицам и для уровня значимости a = 0, 05 равняется 4,74. Так как F_Т > F_крит, то нулевая гипотеза отвергается, и полученное уравнение регрессии принимается статистически значимым.

Оценка статистической значимости коэффициентов регресси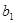и и по t-критерию сводится к сопоставлению численного значения этих коэффициентов с величиной их случайных ошибок и по зависимости

.

Рабочая формула для расчета теоретического значения t – статистики имеет вид

(2.6)

где парные коэффициенты корреляции и коэффициент множественной корреляции рассчитываются по зависимостям:

;

;

;

.

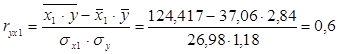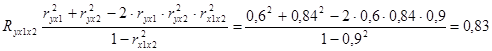Тогда фактические, они же расчетные значения t- статистик соответственно равны

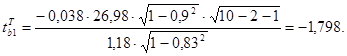
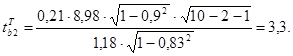
Поскольку критическое значение t- статистики, определенное по статистическим таблицам для уровня значимости a =0,05 равное t_крит =2,36 больше по абсолютной величине чем 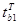= - 1,798, то нулевая гипотеза не отвергается и объясняющая переменная х₁ является статистически незначимой и ее можно исключить из уравнения регрессии. И наоборот, для второго коэффициента регрессии > t_крит (3,3 >2,36), и объясняющая переменная х₂ является статистически значимой.

Для определения средней ошибки аппроксимации воспользуемся зависимостью (3.1.4). Для удобства расчетов преобразуем таблицу 2.8 к виду таблицы 2.9. В данной таблице в колонке 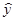рассчитаны текущие значения объясняющей переменной с использованием зависимости (2.3).

Таблица 2.9. К расчету средней ошибки аппроксимации

№ п.п	yi	x1i	x2i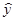
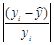
1.	1,50	5,90	5,90	1,93	0,286
2.	5,50	53,10	27,10	4,59	0,165
3.	2,40	18,80	11,20	2,55	0,0625
4.	3,00	35,30	16,40	3,02	0,0006
5.	4,20	71,90	32,50	5,01	0,193
6.	2,70	93,60	25,40	2,69	0,0037
7.	1,60	10,00	6,40	1,88	0,175
8.	2,40	31,50	12,50	2,34	0,025
9.	3,30	36,70	14,30	2,55	0,227
10.	1,80	13,80	6,50	1,76	0,022
S	28,40	370,60	158,20	28,30	1,16

Тогда средняя ошибка аппроксимации равна

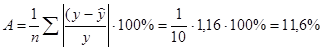
Полученное значение не превышает допустимого предела равного (12…15)%.

Дата добавления: 2014-01-20