Метод Гаусса. Основан данный метод на том, что при замене одного выбранного уравнения системы новым уравнением, полученным прибавлением к обеим частям данного уравнения

О снован данный метод на том, что при замене одного выбранного уравнения системы новым уравнением, полученным прибавлением к обеим частям данного уравнения соответствующих частей другого уравнения, умноженным на одно и то же число, получившееся система будет эквивалентна данной, то есть обе системы будут иметь одно и то же то же решение или одновременно будут неразрешимыми.

Суть метода в том, что последовательно исключаются неизвестные из уравнений системы. Рассмотрим исходную систему. Предположим, что мы хотим исключить переменное 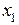из всех уравнений, кроме одного – первого из уравнений системы. В таком случае в качестве первого уравнения в системе мы должны выбрать то, где коэффициент при 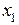отличен от нуля. Предположим, что 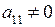. Изменим второе уравнение системы, прибавив к обеим его частям обе части первого уравнения, умноженные на число 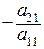. В новом втором уравнении уже не будет члена с 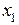. Теперь изменим третье уравнение системы, прибавив к обеим его частям обе части первого уравнения, умноженные на число 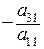. В новом третьем уравнении также не будет члена с 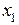…. Проделав эту операцию со всеми уравнениями системы, мы получим новую систему, эквивалентную данной и содержащую 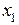только в первом уравнении. Теперь исключим неизвестное 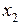из всех уравнений, кроме первого и второго. Для этого на второе место поставим то уравнение системы, не содержащее 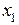, в котором коэффициент при 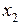не равен нулю. Будем прибавлять обе части этого уравнения, умноженные на соответствующее число, к соответствующим частям всех уравнений, начиная с третьего, чтобы уничтожить в них члены с 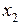….. Проделав это со всеми уравнениями системы и последовательно со всеми неизвестными, мы можем получить следующие варианты эквивалентных систем.

А) В случае, когда 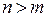, мы либо придем к системе, где последнее уравнение содержит 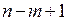неизвестное, либо получим на каком-то этапе невозможное соотношение, когда ноль равен числу, отличному от нуля. В первом случае система имеет бесконечное множество решений, так как первые 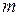неизвестных выражаются линейно через оставшиеся 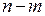неизвестные. Во втором случае система несовместна, то есть, не имеет решений.

Б) В случае, когда 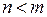, мы можем прийти к системе, в котором 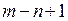последних уравнений одинаковы и представляют собой одно и то же выражение для 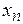. В этом случае система имеет единственное решение. Если же на каком-то этапе получится соотношение, где ноль равен числу, отличному от нуля, то система несовместна.

В) В случае, когда 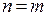, мы также можем на каком-то этапе получить соотношение, где ноль равен числу, отличному от нуля. Такая система несовместна. В противном случае в последнем уравнении определяется неизвестное 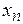, а из предыдущих уравнений определяются последовательно и однозначно все другие неизвестные. В этом случае система имеет единственное решение.

П р и м е р. Решим методом Гаусса систему 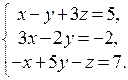Сначала с помощью первого уравнения исключим x из второго и третьего уравнений: к обеим частям второго уравнения прибавим части первого уравнения, умноженные на -3, а к обеим частям третьего уравнения прибавим соответствующие части первого уравнения. Получим эквивалентную систему

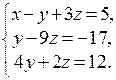Теперь исключим y из последнего уравнения, умножив обе части второго уравнения на -4 и прибавив к обеим частям третьего уравнения. Получим систему с треугольной левой частью: 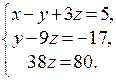Теперь из последнего уравнения мы имеем: 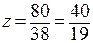. Зная это значение, получим y из второго уравнения: 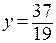. И наконец, значение 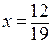определим из первого уравнения.

Для систем, где число уравнений и неизвестных совпадают, возможно применение следующего метода, основанного на вычислении определителей.

Дата добавления: 2014-01-20