Функции многих переменных

Мы знаем способ нахождения наибольшего или наименьшего значения функции одной переменной и способ иллюстрации функциональной зависимости с помощью графика. При решении технических задач часто приходится иметь дело с зависимостью исследуемой величины от многих переменных. Например, 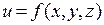– функция трех независимых переменных.

Если график функции одной переменной представляет собой плоскую кривую, характеризующую зависимость функции от переменной, то в случае двух переменных такую характеристику зависимости функции (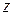) от переменных (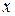и ) выражает поверхность.

Покажем, как изобразить такую поверхность графически, если областью определения функции двух переменных является прямоугольник. Например, построим с помощью пакета программ MAXIMA график функции Для этого введем команду plot3d(x^3-2*y^2,[x,-2,2],[y,-1,1]) инажмем клавиши Shift+Enter. Мы получим следующую картину.

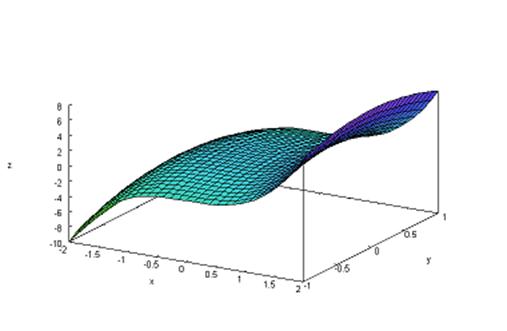
Для графического изображения зависимости функции трех и более переменных понадобилось бы пространство размерности, большей, чем 3. Поэтому такие графические изображения невозможны.

Следовательно, мы должны познакомиться со способом нахождения наибольшего или наименьшего значения функции нескольких переменных без использования визуальной иллюстрации. Большую роль в исследовании функции нескольких переменных играют частные производные.

Дифференцируемость функции двух переменных 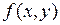в некоторой точке означает, что приращение функции в этой точке отличается от некоторой линейной комбинации приращений каждой из переменных на величину большего порядка малости, чем приращение каждой переменной: 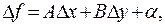где .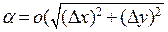

Числа A и B, участвующие в условии дифференцируемости, называются частными производными первого порядка и обозначаются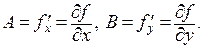

Взять частную производную, например, по переменной x – это значит, считая y постоянной, рассматривать исходную функцию как функцию одной переменной x и взять производную от функции по этой переменной.

Дата добавления: 2014-01-20