Элементы линейного программирования

Задача использования ресурсов.

Для изготовления некоторых видов (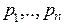) продукции на предприятии используют определенные ресурсы (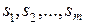). Запасы каждого вида ресурсов на предприятии ограничены (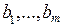). На изготовление каждого изделия 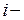го вида продукции идет 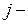й ресурс в объеме 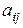, 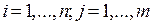. Вопрос: сколько изделий каждого вида продукции следует произвести, чтобы получить наибольшую выручку, если рыночная стоимость одного изделия 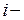го вида продукции равна ?

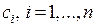Обозначим через 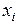количество изделий 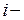го вида продукции. Очевидно, что 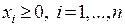. В соответствии с ограниченностью ресурсов 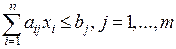. В результате производства мы должны получить максимальную выручку: .

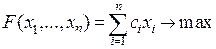Функция 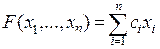называется целевой функцией.

Математическая модель задачи использования ресурсов имеет вид:

,

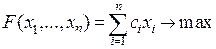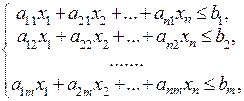
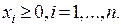
Задачи такого вида, где ищется максимум или минимум линейной функции переменных 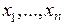при линейных ограничениях составляют предмет изучения раздела «Линейное программирование».

Геометрическая интерпретация задачи использования ресурсов для случая двух переменных.

Предположим, что следует найти максимум функции 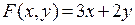при ограничениях: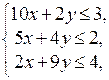 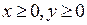. Нарисуем на плоскости XOY область допустимых значений для переменных, заключенную между прямыми .

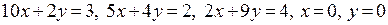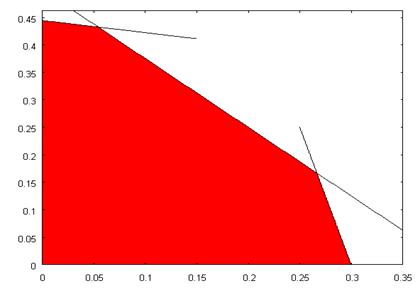
В этой области и следует найти максимальное значение функции 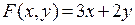. Очевидно, что критических точек линейная функция не имеет. Поэтому максимальное значение находится на границе области. Подставляя в выражение функции линейные зависимости граничных кривых, мы снова получим линейные функции, но уже зависящие от одной переменной. Здесь также максимум достигается в граничных точках. Таким образом, максимум целевой функции достигается в одной из угловых точек нарисованной области. Можно просто перебирать все угловые точки и проверять значения функции в них, а затем отобрать наибольшее. Можно поступить по другому.

Целевая функция принимает нулевое значение в точке (0,0). Проведем через начало координат прямую . Если провести прямую , где 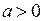, то новая прямая будет параллельна предыдущей и будет проходить правее.

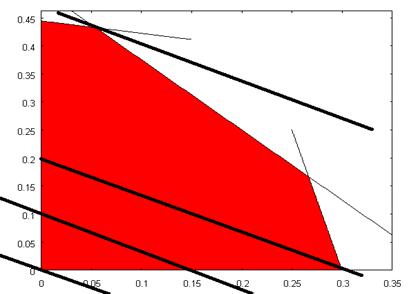
Максимальное значение 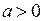, при котором прямая пересекает область допустимых значений переменных, соответствует параллельной прямой, проходящей через одну из вершин. В этой точке и достигается наибольшее значение целевой функции. Сама точка является точкой пересечения прямых 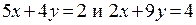, и значит, ее координаты могут быть найдены как решение системы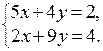

Следует отметить, что если бы целевой функцией была бы функция 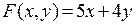, то, двигая параллельно прямую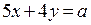, мы совместили бы предельную прямую с одним из граничных отрезков. Значит, во всех точках этого граничного отрезка целевая функция принимала бы одинаковые значения. Таким образом, решение задачи линейного программирования может быть неединственным. Кроме того, существуют задачи, не имеющие решения.

Задача о составлении рациона питания.

Требуется составить экономичный ежедневный рацион питания животного, используя имеющиеся виды кормов (n видов) и не занижая поступления необходимого количества определенных питательных веществ (жиры, белки, углеводы, определенные витамины…– m типов). Обозначим через 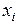количество корма i -го вида, 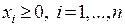. Пусть количество 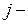го типа питательных веществ в единице массы корма i -го вида равно 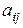. Обозначим через 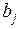минимум массы питательного вещества 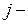го типа, обязанного содержаться в ежедневном рационе. Пусть стоимость единицы массы кормов i -го вида равна 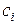. Тогда мы придем к следующей задаче

,

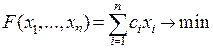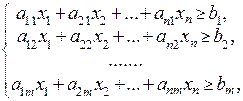
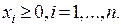
В случае функции 2-х переменных ее также можно решать графическим методом.

В производственных задачах бывает очень много переменных, и графический метод там неприменим. Часто применяют так называемый симплексный метод – перебор угловых точек многомерной области допустимых значений в многомерном пространстве. В настоящее время пакеты программ содержат готовые алгоритмы решения задач линейного программирования симплексным методом. Покажем, как это работает в пакете MAXIMA.

Предположим, что нам необходимо найти решение следующей задачи

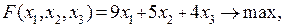
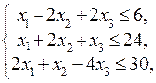
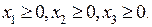
В этом случае следует набрать следующие команды: load("simplex");

maximize_lp(9*x1+5*x2+4*x3,[x1-2*x2+2*x3<=6,x1+2*x2+x3<=24,2*x1+x2-4*x3<=30,x1>=0,x2>=0,x3>=0]) и нажать Shift+Enter. Ответ компьютер выдаст в виде [152,[x3=2/3,x2=14/3,x1=14]]. Это значит, что наибольшее значение, равное 152, целевая функция принимает в точке (14,14/3,2/3).

Дата добавления: 2014-01-20