ТЕМА №1

ОСНОВЫ МОДЕЛИРОВАНИЯ

СОЦИАЛЬНО- ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ.

1. Понятие социально- экономических систем и процессов.

2. Понятие модели, классификация моделей.

3. Моделирование, его виды.

4. Принципы моделирования.

5. ЭММО, ее особенности и задачи. Типы ЭММО.

6. Этапы построения ЭММО.

7. Основные элементы базовой модели.

8. Формы записи ЭММ.

1. Понятие социально- экономических систем и процессов.

Под процессом понимается любой вид движения, модификации, трансформации, чередования или эволюции, любое изменение изучаемого объекта в течение определенного времени, будь то изменение его места в пространстве, либо модификация его количественных и качественных характеристик. Экономические процессы в различных отраслях национального хозяйства представляют собой сложные явления, связанные с многочисленными факторами внутреннего и внешнего воздействия на производство, которые изменяются с течением времени. Социально-экономические процессы – это совокупность естественных и общественных процессов (либо реальных и виртуальных процессов), которые формируются на основе их интеграции и сбалансированного воздействия рыночного и институционального регулирования на управляемую социально-экономическую систему.

Система – это совокупность составляющих элементов и взаимосвязей между ними. Социально-экономическая система – сложная система, в которой взаимодействуют экономические, технические и социальные процессы, постоянно изменяющиеся под воздействием внешних условий, в том числе и научно-технического прогресса. Социально-экономической системой называется сложная вероятностная динамическая система, охватывающая процессы производства, обмена, распределения и потребления материальных и других благ. Она относится к классу кибернетических систем, т. е. систем управляемых.

Среди социально-экономических систем целесообразно выделить производственную систему (ПС), которая, в отличие от систем других, содержит в качестве важнейшего элемента сознательно действующего человека, выполняющего функции управления (принятие решений и их контроль). В соответствии с этим в качестве производственной системы могут рассматриваться различные подразделения предприятий, сами предприятия, научно-исследовательские и проектные организации, объединения, отрасли и, в отдельных случаях, народное хозяйство в целом. Объектом управления на предприятии выступают несколько групп функциональных процессов: маркетинг, исследования и разработки, производство, финансы, персонал и др.

2. Понятие модели; классификация моделей.

Термин «модель» - от латинского modulus – образец, норма, мера. Модель - мысленно- представляемый объект- копия, который в процессе исследования замещает объект –оригинал таким образом, что его непосредственное изучение дает новые знания об объекте- оригинале. Понятие модели основано на принципе аналогии.

Один и тот же объект может быть описан различными моделями в зависимости:

• от взглядов и мировоззрения специалистов;

• исследовательской и практической потребности;

• возможностей математического аппарата;

• возможностей вычислительной техники;

• структуры информационного обеспечения и т. д.

Макроэкономические модели описывают экономику государства как единое целое, связывая между собой укрупненные (агрегированные) материально вещественные и финансовые показатели: валовой национальный продукт, национальный доход, совокупный спрос, совокупное потребление, инвестиции, занятость, инфляцию, процентную ставку, количество денег и т.д.

Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики либо хозяйственное поведение отдельной такой составляющей (отрасли, региона, фирмы, потребителя и т.п.).

Статистические мо дели – это модели, в которых значения всех параметров относятся к одному кванту (моменту или периоду) времени.

Динамические модели – это модели, у которых параметры изменяются во времени.

Теоретические модели предназначены для изучения общих закономерностей и свойств рассматриваемой экономической системы.

Прикладные модели дают возможность определять и оценивать параметры функционирования конкретных экономических объектов и формулировать рекомендации для принятия практических хозяйственных решений.

3. Моделирование, его виды.

Процесс построения модели называется моделированием. Моделирование – научный метод исследования систем, рассматриваемых как оригиналы на их аналогах –моделях с целью углубления знаний и для распространения этих знаний на систему – оригинал при управлении ее поведением.

Информационное – для наглядного изображения составных частей и связей объектов: схемы, чертежи, графики, планы (квартиры), карты (географические).

Геометрическое – передает пространственные формы объекта, их пропорции: макеты зданий, сооружений.

Образное – это выражение свойств оригинала с помощью образов: рисунки, художественные полотна, фотографии, кинофильмы.

Знаковое- использует алфавиты формальных языков: условные знаки, специальные символы, буквы, цифры (например, физические и химические формулы, математические выражения, нотная запись).

Вербальное – мысленная модель, выраженная в разговорной форме: литературные произведения, инструкции пользования устройством, правила дорожного движения.

4. Принципы моделирования.

1. Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации ее моделирование лишено смысла. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена ее адекватная модель.

2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля, и за конечное время. Обычно задают некоторое пороговое значение P0 вероятности достижения цели моделирования P(t), а также приемлемую границу t0 времени достижения этой цели. Модель считают осуществимой, если может быть выполнено условие P(t0) ≥ P0.

3. Принцип множественности моделей. Данный принцип, несмотря на его порядковый номер, является ключевым. Речь идет о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели признаются лишь некоторые стороны реальности. Для более полного ее исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемые процесс.

4. Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования.

5. Принцип параметризации. В ряде случаев моделируемая система имеет в своем составе некоторые относительно изолированные подсистемы, характеризующиеся определенным параметром, в том числе векторным. Такие подсистемы можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объем и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели.

5. ЭММО, ее особенности и задачи. Типы экономико- математических моделей.

Формализованное представление закономерностей поведения реальных экономических систем в виде абстрактных экономических аналогов – системы уравнений и неравенств – получило название математического моделирования.

По В.С. Немчинову, экономико-математическая модель представляет собой концентрированное выражение наиболее существенных взаимосвязей и закономерностей поведения управляемой системы в математической форме.

Математическая модель по сравнению с реальным физическим экспериментом обладает некоторыми преимуществами, связанными с тремя ее основными особенностями:

· экономией материальных ресурсов, требуемых для постановки и проведения физического эксперимента;

· возможностью апробации системы в изменяющихся по воле экспериментатора условиях;

· оценкой работоспособности систем с длительными технологическими циклами в существенно сжатые сроки.

Практическими задачами экономико-математического моделирования являются:

· анализ экономических процессов;

· экономическое прогнозирование, предвидение развития экономических процессов;

· выработка управленческих решений на всех уровнях хозяйственной иерархии.

Результаты экономико-математического моделирования могут рассматриваться как готовые управленческие решения или как «консультирующие» средства. Принятие управленческих решений остается за человеком. Экономико-математическое моделирование применяется при решении таких проблем, как разработка наиболее выгодного ассортимента при ограниченных ресурсах, расчет оптимальной величины товарных запасов, планирование маршрутов движения сбытовых агентов и др.

Выделяют три основных типа экономико-математических моделей:

Ø модели межотраслевого баланса (отражают систему взаимоузявки различных отраслей народного хозяйства по производству и распределению продукции в виде шахматных квадратных матриц);

Ø экономико-статистические модели (корреляционно-регрессионные уравнения связей результативного и факторного признаков, производственные функции);

Ø оптимизационные модели (модели выбора оптимального варианта при заданных условиях, в основе методы математического программирования).

6. Этапы построения ЭММО.

1. Исследование моделируемого объекта

Производится качественный и количественный анализ объекта и ситуаций, имеющих к нему отношений. Сложные объекты разбиваются на части (элементы), определяются связи этих элементов, их свойства и т.д.

2. Постановка задачи

Наиболее ответственный момент, предполагает четкую экономическую формулировку: экономическую цель, установление продолжительности планового периода, выяснение известных параметров объекта и тех, количественное значение которых нужно определить, основные факторы и условия, отражающие их связи в моделируемом объекте.

3. Выбор модели и метода решения

Как правило, решаемые в экономической практике задачи стандартизованы и реализуются в известную математическую модель, алгоритм решения которой известен.

4. Построение числовой экономико- математической модели

Осуществляется построение математической модели объекта с использованием статистической, нормативно- справочной и прогнозной информации. На основе исходных данных разрабатываются коэффициенты модели.

5. Разработка или выбор программного обеспечения.

Для стандартных задач осуществляется выбор подходящего пакета прикладных программ- SIMPLEX, EXCEL.

6. Решение задачи на ЭВМ.

Происходит отыскание математически допустимого решения. Здесь может обнаружиться несовместимость системы ограничений, которая устраняется корректировкой исходной модели. Если результат решения задачи удовлетворяет поставленным целям, то план оптимален, если не удовлетворяет, то необходимо вернуться на начальный этап решения.

7. Анализ оптимального решения.

Полученные результаты оцениваются с помощью двойственных оценок или теневых цен. Делается вывод об адекватности модели и приемлемости результатов моделирования.

8. Рекомендации по управлению объектом.

Какие управленческие решения (приказы, распоряжения, перемещения и в какие сроки, в какой последовательности, с какой этапностью) нужно предпринять, чтобы перейти от фактического (худшего) состояния к оптимальному (лучшему), каких затрат это потребует, как окупятся затраты.

7. Основные элементы базовой модели.

Базовая модель включает в себя следующие элементы:

· Переменные;

· Ограничения;

· Коэффициенты переменных в ограничениях;

· Целевая функция.

Необходимо выделять основные и вспомогательные переменные. Основные – это переменные по растениеводству и животноводству, которые означают размер отрасли (с-х культуры, отрасли животноводства, с-х технику, минеральные удобрения, виды кормов, т.е. те величины, которые определяют основное содержание моделируемого процесса в каждом конкретном случае, виды или способы деятельности, размеры которых требуется определить). Если основные переменные разбиваются на отдельные переменные, связанные с технологией выращивания, способами использования, то это тоже основные переменные. Вспомогательные переменные необходимы для точной и удобной математической формулировки задачи (общее количество кормовых единиц, рабочая сила со стороны и т.д.).

· единицы измерения выбираются одинаковые для однотипных переменных. Нужно следить, чтобы в правой и левой частях ограничения единицы измерения совпадали;

· ограничения подразделяются на основные, дополнительные и вспомогательные. Основные ограничения выражают главные, наиболее существенные условия задачи. Они накладываются на все или большинство переменных моделей. К основным относятся ограничения по использованию производственных ресурсов(земли, рабочей силы, удобрений, кормов и т.д.). Дополнительные ограничения накладываются на небольшое количество переменных величин или отдельные переменные. Обычно они формулируются в виде неравенств, ограничивающих снизу и сверху потребление животными отдельных групп кормов, объемы производства некоторых видов продукции, удельный вес культур в полях севооборота и др. При этом не следует перегружать модель дополнительными ограничениями, т.к. это приведет к сужению области допустимых значений. Все ограничения можно разделить на ограничения по производственным ресурсам типа £, по производству продукции типа ³, ограничения балансового типа = (например, ограничение по определению общих затрат материальных средств). Вспомогательные ограничения вводятся для правильности формулировки задачи. Самостоятельного экономического значения не имеют. С их помощью могут быть записаны условия пропорциональной связи между переменными и их группами. Система ограничений- условия задачи, сформулированные в математической форме.

Коэффициенты переменных в ограничениях. В их качестве может выступать исходная информация для задачи или приобретенная информация. ТЭК разделяют на:

1. коэффициенты затрат f_ls

2. коэффициенты выпуска V_gs

3. коэффициенты пропорциональности.

Целевая функция – максимизация доходного показателя или минимизация затратного, должна быть единственной, но можно предусмотреть варьирование целей при планировании модельного эксперимента. Критерий оптимальности определяет качество функционирования исследуемой системы или объекта.

8. Формы записи ЭММО.

а) Структурная модель.

Записывается с помощью общепринятых обозначений, в качестве которых используют буквы латинского, греческого алфавита, заглавные и строчные.

б ) Числовая запись.

Буквенные обозначения заменяются на числа.

Числовую модель в развернутой форме записывают, если размерность общей модели невелика (20-30 переменных и ограничений). Если размерность общей задачи большая, то вместо числовой модели записывают матрицу коэффициентов на клетчатой (миллиметровой) бумаге.

Матричная запись - таблица числовых коэффициентов, в которых столбцы имеют наименования- обозначения переменных, а строки перенумерованы в соответствии с количеством всех ограничений. Последней строкой записываются коэффициенты целевой функции, последним столбцом- свободные члены ограничений (со знаком отношения ³ £).

Лекция №3

1. Поиск решений

Мощным средством анализа данных Excel является надстройка Solver (Поиск решения). С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.

Программа Поиск решений (в оригинале Excel Solver) – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных и нелинейных задач оптимизации, используется с 1991 года.

Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями:

· количество неизвестных (decision variable) – 200;

· количество формульных ограничений (explicit constraint) на неизвестные – 100;

· количество предельных условий (simple constraint) на неизвестные – 400.

Высокая эффективность их применения объясняется интеграцией программы оптимизации и табличного бизнес-документа. Благодаря мировой популярности табличного процессора MS Excel встроенная в его среду программа Solver является наиболее распространенным инструментом для поиска оптимальных решений в сфере современного бизнеса.

Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи. Если в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите команду Сервис → Надстройки и активизируйте надстройку Поиск решения. Если же этой надстройки нет в диалоговом окне Надстройки, то необходимо обратиться к панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ и с помощью программы установки Excel (или Office) установить надстройку Поиск решения.

2. Технология решения ЗЛП в среде Excel с помощью поиска решений

Для решения задачи необходимо:

1. Создать форму для ввода условий задачи.

2. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).

3. Ввести исходные данные.

4. Ввести зависимости для ограничений и целевой функции.

5. Указать назначение целевой функции (установить целевую ячейку).

6. Ввести ограничения.

7. Ввести параметры для решения задачи линейного программирования.

Ввод зависимостей для ограничений и целевой функции осуществляется через запись формул. Для этого используется Мастер функций, Категория – Математические, Функция – СУММПРОИЗВ.

Пункты 5 – 7 выполняются в диалоговом окне Поиска решения. После выбора команды Сервис → Поиск решения появится диалоговое окно Поиска решения, в котором есть три параметра:

¾ Установить целевую ячейку

¾ Изменяя ячейки

¾ Ограничения

Установить целевую ячейку. Во всех задачах для средства Поиск решения оптимизируется результат в одной из ячеек рабочего листа. Целевая ячейка связана с другими ячейками этого рабочего листа с помощью формул. Средство Поиск решения использует формулы, которые дают результат в целевой ячейке, для проверки возможных решений. Можно выбрать поиск наименьшего или наибольшего значения для целевой ячейки или же установить конкретное значение.

Изменяя ячейки. Изменяемые ячейки – это те ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в целевой ячейке. Для поиска решения можно указывать до 200 изменяемых ячеек. К изменяемым ячейкам предъявляются два основных требования: они не должны содержать формул, и изменение их значений должно отражаться на изменении результата в целевой ячейке.

Ограничения. Ввод и редактирование ограничений осуществляется в диалоговом окне Добавление ограничений, для чего используются кнопки Добавить, Изменить. Для удаления ограничений используется кнопка – Удалить.

Ввод параметров решения ЗЛП осуществляется в окне параметры поиска решения, вызываемом кнопкой Параметры. Установка флажка Линейная модель, обеспечивает применение симплекс-метода. Условие неотрицательности переменных достигается в решении ЗЛП путем установки флажка Неотрицательные значения.

После установки Параметров поиска решения на экране опять появится диалоговое окно Поиск решения. Чтобы осуществить решение задачи, нужно выбрать команду Выполнить.

3. Параметры средства Поиск решения

Максимальное время - служит для ограничения времени, отпущенного на поиск решения задачи. В этом поле можно ввести время в секундах, не превышающее 32 767 (примерно девять часов); значение 100, используемое по умолчанию, вполне приемлемо для решения большинства простых задач.

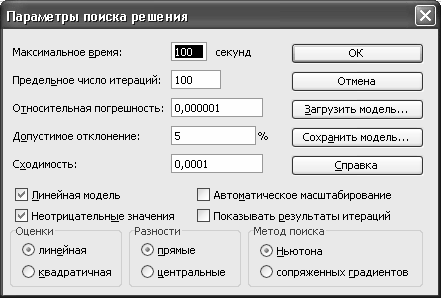
Предельное число итераций - управляет временем решения задачи путем ограничения числа вычислительных циклов (итераций).

Относительная погрешность - определяет точность вычислений. Чем меньше значение этого параметра, тем выше точность вычислений.

Допустимое отклонение - предназначен для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. Чем больше значение допуска, тем меньше времени требуется на поиск решения.

Сходимость - применяется только к нелинейным задачам. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается.

Линейная модель - служит для ускорения поиска решения путем применения к задаче оптимизации линейной модели. Нелинейные модели предполагают использование нелинейных функций, фактора роста и экспоненциального сглаживания, что замедляет вычисления.
Неотрицательные значения - позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых не было задано соответствующее ограничение в диалоговом окне Добавить ограничение.

Автоматическое масштабирование - используется, когда числа в изменяемых ячейках и в целевой ячейке существенно различаются.

Показывать результаты итераций - приостанавливает поиск решения для просмотра результатов отдельных итераций.

Загрузить модель - после щелчка на этой кнопке отрывается одноименное диалоговое окно, в котором можно ввести ссылку на диапазон ячеек, содержащих модель оптимизации.

Сохранить модель - служит для отображения на экране одноименного диалогового окна, в котором можно ввести ссылку на диапазон ячеек, предназначенный для хранения модели оптимизации.

Оценка линейная - выберите этот переключатель для работы с линейной моделью.

Оценка квадратичная - выберите этот переключатель для работы с нелинейной моделью.

Разности прямые - используется в большинстве задач, где скорость изменения ограничений относительно невысока. Увеличивает скорость работы средства Поиск решения.

Разности центральные - используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдано сообщение о том, что получить более точное решение не удается.

Метод поиска Ньютона - требует больше памяти, но выполняет меньше итераций, чем в методе сопряженных градиентов.

Метод поиска сопряженных градиентов - реализует метод сопряженных градиентов, для которого требуется меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно большая и необходимо экономить память или если итерации дают слишком малое отличие в последовательных приближениях.

4. Создание отчета по результатам поиска решения

Excel позволяет представить результаты поиска решения в форме отчета. Существует три типа таких отчетов:

Результаты. В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях.

Устойчивость. Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.

Пределы. Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

Чтобы их вывести отчеты, необходимо выделить их название, нажатие ОК – сформирует отчеты на отдельных листах рабочей книги.

По найденным результатам можно создавать отчеты. Такие отчеты полезны для сравнения влияния на решение различных ограничений или исходных данных. Потому они являются очень важными инструментом для анализа полученных результатов и последующего их улучшения в зависимости от возможностей и ресурсов предприятия.

Дата добавления: 2014-01-20