Математические модели задач линейного программирования

Рассмотрим детерминированные линейные задачи, в которых показатель эффективности W=W(a, x) линейнозависит от заданных условий a и элементов решения x=(x₁, x₂, …, x_n).

Такие задачи составляют группу задач линейного программирования.

Задача о пищевом рационе.

Каждому человеку для нормальной жизнедеятельности необходимо определенное количество белков (b₁), жиров (b₂), углеводов (b₃) и витаминов (b₄). Рассмотрим N видов продуктов.

	Продукт	Белки	Жиры	Углеводы	Витамины	Цена
	П1	а11	а12	а13	а14	с1
	П2	а21	а22	а23	а24	с2
N	ПN	аN1	аN2	аN3	аN4	сN

Математическая модель.

ДАНО: x_i – количество единиц i- продукта.

Суммарная стоимость продуктов – показатель эффективности.

НАЙТИ решение Х= (x₁, x₂,…, x_N), которое удовлетворяет следующей системе неравенств:

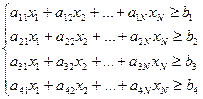
и обращает в минимум показатель эффективности

ПРИМЕР 2.1.

Имеется 5 видов продуктов питания заданной калорийности. Необходимо составить рацион на неделю с максимальным количеством калорий, уложившись в сумму 1000 руб. Количество каждого продукта не должно превышать заданной нормы.

Показатели	Номер вида продукта
Относительная калорийность на 1 кг продукта
Цена 1 кг продукта, руб.
Норма потребления продукта, кг

Математическая модель.

x_i – количество продуктов i-ого вида

x₁ ≤ 10

x₂ ≤ 15

x₃ ≤ 20

x₄ ≤ 10

x₅ ≤ 15

5x₁ + 10x₂ + 15x₃ + 20x₄ + 30x₅≤1000

W = 10x₁ + 10x₂ + 15x₃ + 30x₄ + 20x₅ →max

Задача производственного планирования.

Пусть имеется некоторый экономический объект (предприятие, бригада, АОО), который может производить продукцию n видов. В процессе производства допустимо использование m видов ресурсов. На производство единицы продукции j- го вида ресурсов i- го вида требуется в количестве а_ij. Технологию предприятия можно представить как прямоугольную матрицу m на n. Если план производства представить в виде вектора х=(х₁, х₂, …, х_n), тогда общие затраты ресурса i- го вида будут равны 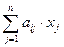. Всякая реальная система имеет ограничения на ресурсы. Представим их в виде вектора b=(b₁, b₂, …, b_m). В математической форме по правилам матричной алгебры система условий будет иметь вид: Ах≤b. По каждому виду изделия объем не должен превышать спрос v=(v₁, v₂, …, v_n): x≤.v Также необходимо добавить ограничения на неотрицательность элементов решения: х ≥ 0.

Обозначим за с_j цену единицы продукции j –го вида. Тогда в качестве целевой функции можно выбрать функцию f(x) = 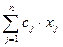= cx. Ее необходимо максимизировать.

ПРИМЕР 2.2.

Ткацкая фабрика лилипутов выпускает 2 вида ткани. Изучение спроса показало, что ежедневно необходимо выпускать не меньше 8м ткани. Суточный расход сырья не должен превышать 10ед. Установить план выпуска ткани с максимальной прибылью, при условии полного удовлетворения спроса.

Показатели	Вид ткани
Сырьё, ед/м
Доход, у.е./м

Математическая модель:

х _i – количество ткани i -го вида (м)

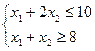
х_i ³0

L= х₁+х₂Þmax

Дата добавления: 2014-01-20