Максимальный поток на сети

2 5

РЕШЕНИЕ:

Гамильтоновы циклы

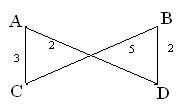
Граф задан в форме матрицы, где в ячейках задана стоимость передвижения между пунктами. На главной диагонали ставится символ ∞, чтобы исключить бессмысленный путь в сам себя.

	A	B	C	D	min
A	∞
B		∞
C			∞
D				∞

1.1. Найдем в каждой строке матрицы минимальный элемент и вычтем его из всех элементов этой строки.

	A	B	C	D
A	∞
B		∞
C			∞
D				∞
min

Т.к. в полученной матрице оказался столбец без нулевых элементов, то найдем в нем минимальный элемент и вычтем его из всех элементов этого столбца.

	A	B	C	D
A	∞
B		∞
C			∞
D				∞

Просуммируем все вычтенные элементы и получим нижнюю границу цикла в= 2+2+3+2+1=10

1.2. Проведём оценку всех нулевых элементов матрицы.

γ_АВ=0+0=0

γ_АС=0+2=2

γ_AD=0+0=0

γ_BА=0+0=0

γ_BD=0+0=0

γ_CA=0+2=2

γ_DA=0+0=0

γ_DB=0+0=0

Оценку нулей удобно представлять в таблице.

	A	B	C	D
A
B
C
D

Выберем максимальную из оценок θ=max γ=γ_АC=2

1.3. Множество путей разобьём на два подмножества:Q AC – пути, содержащие дугу (AC) и Q AC – пути, не содержащие дугу (АC). Для второго подмножества нижней границей будет: в^/=в+ θ =10+2=12.

Чтобы вычислить границу для первого подмножества, перейдём к матрице на порядок ниже, вычеркнув A-строку и C-столбец. В новой матрице для исключения обратного пути (CA) в соответствующую клетку поставим знак ∞.

	A	B	D	min
B		∞
C	∞
D			∞

Преобразуем матрицу аналогично п.1.1

	A	B	D
B		∞
C	∞
D			∞

Вычислим границу полученной матрицы 2+0=2

и добавим её к нижней границе цикла. Эта сумма в^//=10+2=12 и будет границей для первого подмножества.

1.4. Сравним границы всех висячих вершин и выберем вершину с наименьшей границей. Если этих вершин две, выбираем любую из них. Это вершина Q AC, нижняя граница которой =12.

	A	B	D
B		∞
C	∞
D			∞

1.5. Проведём оценку всех нулевых элементов матрицы.

	A	B	D
B
C
D

Выберем максимальную из оценок θ=max γ=γ_BD=3

в^/=12+3=15.

1.6. Все последующие пункты выполняем аналогично предыдущим.

	A	B
C	∞
D		∞

Оценка нулей:

	A	B
C		∞
D	∞

Выберем максимальную из оценок θ=max γ=γ_СB= ∞

в^/=в+ θ=∞

	A
D

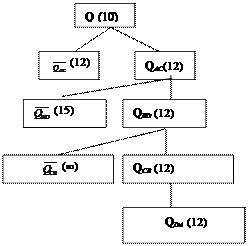Все строки и столбцы этой матрицы содержат нули. Следовательно, граница остается равной 12.

ЗАДАЧА. Найти величину максимального потока на транспортной сети.

ПОСТАНОВКА ЗАДАЧИ.

Рассмотрим транспортную задачу на сети (I,D,G) с заданными пропускными способностями дуг c(i,j).

Выделим две фиксированные вершины: s - источник и t – сток. Потоком на сети s→t назовем числовую функцию f, определенную на множестве дуг и удовлетворяющую следующим линейным уравнениям и неравенствам:

0≤ f(i,j) ≤c(i,j) для любых (i,j)

Требуется максимизировать переменную x

Разрезом L в сети, отделяющим вершины s t называется множество дуг

Любой путь s→t содержит по крайней мере одну дугу разреза.

КРИТЕРИЙ ОПТИМАЛЬНОСТИ: на реальной сети величина произвольного потока не превосходит пропускной способности разреза, а величина максимального потока равна минимальной пропускной способности разреза.

Пропускная способность исходящих дуг (Р,Т) и (М,К) превышает суммарную пропускную способность входящих в соответствующую вершину дуг. Для того, чтобы сеть стала реальной, заменим с(Р,Т)=4, с(М,К)=8. Найдем и вычислим значение пропускных способностей всех разрезов. (К,В) – (Т,В) разрез с минимальной пропускной способностью =10. Следовательно, максимальный поток х=10

ПРИМЕР 3.12.

М 9 К

8 4 3

А

3 1 2 2 7 В

Р 5 Т

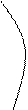
М 8 К

8 4 3

А

3 1 2 2 7 В

Р 4 Т

ПРИМЕР 3.13.

М 2 К

8 2 1

А 1 2 В

3 2 7

Р 1 Т

РЕШЕНИЕ :

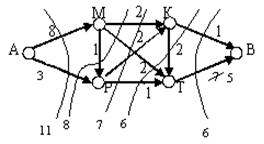
Пропускная способность исходящей дуги (Т,В) превышает суммарную пропускную способность входящих в соответствующую вершину дуг. Для того, чтобы сеть стала реальной, заменим с(Т,В)=5.

Найдем и вычислим значение пропускных способностей всех разрезов. (К,В) – (Т,В) разрез с минимальной пропускной способностью =6. Следовательно, максимальный поток =6.

Сеть, имеющую несколько источников и стоков можно свести к сети с одним источником и стоком.

ПРИМЕР. Пусть имеется несколько источников S и стоков T (транспортная задача). Расширим сеть, добавив два узла s*, t* и все дуги (s*, S), (T,t*). Доопределим функцию пропускной способности, положив

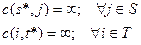
МЕТОД РАССТАНОВКИ ПОМЕТОК.

1. Начальный поток f(i,j) = 0.
Припишем вершинам данной сети пометки, которые будут иметь вид (i+, ε) или
(i^-, ε). Источник пометим (-, ∞), т.е. ε(s)= ∞.

2. Для любой помеченной вершины i выберем все непомеченные вершины j для которых f(i,j)<c(i,j) и припишем им пометки (i+, ε(j)), где ε(j)=min[ε(i), f(i,j)]. Тем вершинам, которые останутся непомеченными, но для которых f(i,j)>0, приписываем пометку (i-, ε(j)).

Эту операцию повторяем до тех пор, пока не окажется помеченным сток. Если сток остался непомеченным, то найденный поток - максимальный, а множество дуг, связывающих помеченные вершины с непомеченными, образуют минимальный разрез.

3. Пусть сток имеет пометку (j+, ε(t)), тогда f(j,t) заменяем на f(j,t)+ε(t). Если же сток имеет пометку (j-, ε(t)), то f(j,t) заменяем на f(j,t)-ε(t). Переходим к вершине j. Если j имеет пометку (i+, ε(j)), то заменяем f(i,j) на f(i,j)+ε(t), а если ­ (i-, ε(j)), f(j,i) заменяем на f(j,i)-ε(t). Переходим к вершине i. Эту операцию повторяем до тех пор, пока не достигнем источника s. Изменение потока прекращается, стираются все пометки и переходим к п.2

ПРИМЕР 3.14.

М 4 К

8 4 3

А

3 1 2 4 7 В

Р 5 Т

1 шаг	А → (-, ∞) М → (А+,8) Р → (А+,3) К → (Р+,3) Т → (Р+,3) В → (Т+,3)	f(Т,В)=3 f(Р,Т)=3 f(А,Р)=3 f(Р,К)=0 f(А,М)=0 f(М,Р)=0 f(М,К)=0 f(М,Т)=0 f(К,Т)=0 f(К,В)=0
2 шаг	А → (-, ∞) М → (А+,8) Р → (М+,1) К → (М+,4) Т → (М+,2)	f(К,В)=3 f(М,К)=3 f(А,М)=3 f(Т,В)=3 f(Р,Т)=3 f(А,Р)=3 f(Р,К)=0 f(М,Т)=0 f(М,Р)=0 f(К,Т)=0
3 шаг	А → (-, ∞) М → (А+,5) Р → (М+,1) К → (М+,1) Т → (М+,2) В → (Т+,2)	f(Т,В)=5 f(М,Т)=2 f(А,М)=5 f(К,В)=3 f(М,К)=3 f(Р,Т)=3 f(А,Р)=3 f(Р,К)=0 f(М,Р)=0 f(К,Т)=0
4 шаг	А → (-, ∞) М → (А+,3) Р → (М+,1) К → (М+,1) Т → (Р+,1) В → (Т+,1)	f(А,М)=6 f(Т,В)=6 f(Р,Т)=4 f(М,Р)=1 f(М,Т)=2 f(К,В)=3 f(М,К)=3 f(А,Р)=3 f(Р,К)=0 f(К,Т)=0
5 шаг	А → (-, ∞) М → (А+,2) Р → (М-,1) К → (М+,1) Т → (К+,1) В → (Т+,1)	f(А,М)=7 f(М,К)=4 f(К,Т)=1 f(Т,В)=7 f(Р,Т)=4 f(М,Р)=1 f(М,Т)=2 f(К,В)=3 f(А,Р)=3 f(Р,К)=0
6 шаг	А → (-, ∞) М → (А+,1)	Поток оптимален f=10 Минимальный разрез:М → Т-М → Р-М → К

ЗАДАЧА. Найти наибольший поток на сети

АЛГОРИТМ

Обозначим вершину s= х₀. Все остальные – х_i.

1 этап.

1. Выбираем любой путь, все дуги которого не насыщены.

2. Увеличиваем величину потока по этому пути на единицу до тех пор, пока в нем не будет насыщенной дуги.

Процесс увеличения потока продолжаем до тех пор, пока не будет построен полный поток, т.е. любой путь будет содержать хотя бы одну насыщенную дугу.

2 этап.

1. Помечаем х₀ индексом 0.

2. Если х_i уже помеченная вершина, то помечаем (+i) все непомеченные вершины, в которые идут не насыщенные дуги из х_i, и индексом (–i) все непомеченные вершины, из которых идут дуги с ненулевым потоком в х_i.

3. Если в результате этого процесса окажется помеченной вершина t, то между s и t найдется путь, все вершины которого помечены номерами предыдущих вершин. Поток во всех дугах этого пути увеличиваем на единицу, если при движении от s к t ориентация дуги совпадает с направлением движения, и уменьшаем на единицу, если дуга имеет противоположную ориентацию. Переходим к п.1.

4. Когда вершину t невозможно пометить процесс прекращается и полученный поток является наибольшим потоком сети.

ПРИМЕЧАНИЕ. Перейти к 2 этапу можно, не завершая первого этапа (см. пример 3.16).

ПРИМЕР 3.15.

9

8 4 3

s 1 2 t

3 2 7

РЕШЕНИЕ:

На заданной транспортной сети найден полный поток. Насыщенные дуги выделены

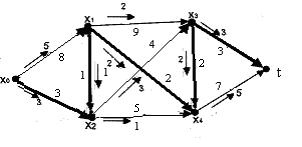
Пометим сеть и увеличим в ней поток согласно алгоритму. Получим

В этой сети также можно пометить конечную вершину, причем результат разметки окажется тем же самым. Изменив поток, получим сеть, в которой конечную вершину пометить невозможно, поэтому поток в ней является наибольшим и равен 10.

ПРИМЕР 3.16.

8 2 1

s 1 2 t

3 2 7

РЕШЕНИЕ.

На заданной транспортной сети найден неполный поток

Пометим сеть и увеличим в ней поток согласно алгоритму. Получим

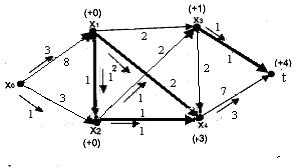
В этой сети также можно пометить конечную вершину, причем результат разметки окажется тем же самым. Изменив поток, получим сеть, в которой конечную вершину пометить невозможно, поэтому поток в ней является наибольшим и равен 6.

Раздел IV. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ.

Динамическое программирование служит для поиска оптимальных многоэтапных решений. Например, долгосрочное планирование замены оборудования; деятельность отрасли промышленности в течение ряда лет. Оно использует принцип оптимальности, согласно которому всякое новое частичное решение должно быть оптимальным относительно достигнутого состояния.

Лучше много раз решить одну простую задачу, чем один раз сложную.

ЗАДАЧА 1. О наивыгоднейшем пути между двумя пунктами.

Требуется соорудить путь, соединяющий два пункта А и В, из которых второй лежит к северо-востоку от первого. Для простоты допустим, что прокладка пути состоит из ряда шагов, и на каждом шаге мы можем двигаться либо строго на север, либо строго на восток. Тогда любой путь представляет собой ступенчатую ломаную линию, отрезки которой параллельны одной из координатных осей. Затраты на сооружение каждого из таких отрезков известны.

ПРИМЕР 4.1. Найти минимальный путь от А до В.

2 4 В

3 1 3

2 3

2 5 2

2 3

А

Последний шаг – достижение т.В. Перед последним шагом мы могли находиться в точках, откуда за один шаг можно достичь т.В. Таких точки две (система могла находиться в одном из двух состояний). Для каждой из них существует единственный вариант достижения т.В: для одной – двигаться на восток; для другой – на север. Запишем затраты 4 и 3 в каждом случае.

4

Теперь оптимизируем предпоследний шаг. После предыдущего шага мы могли оказаться в одной из трех точек: С₁, С₂, С₃.

Для т. С₁ существует единственное управление (пометим его стрелкой) – двигаться на восток, при этом затраты составят 2(на данном шаге)+4(на следующем шаге)=6. Аналогично для т. С₃ затраты составят 2+3=5. Для т.С₂ существует два управления: идти на восток или на север. В первом случае затраты составят 3+3=6, а во втором случае – 1+4=5. Значит условное оптимальное управление – идти на север. Пометим его стрелкой и занесем соответствующие затраты.

2 4

С₁

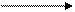
1 3

3

С₂

С₃

Далее «пятясь» от предпоследнего шага к первому, найдем оптимальные управления на каждом шаге (обозначим их стрелкой) и условный оптимальный расход (запишем его). Теперь прочитаем рекомендации на каждом шаге (куда указывают стрелки), начиная с первого (от т.А) и получим оптимальный путь. Затраты на его сооружение W=9

2 4

3 1 3

2 3

2 5 2

2 3

ЗАДАЧА 2. О загрузке машины (о рюкзаке).

Имеется N предметов. Известны вес a_i и ценность φ_i каждого предмета. Требуется заполнить рюкзак, способный вместить вес ≤ R, таким набором предметов, который обладал бы наибольшей ценностью.

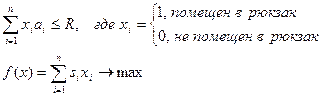
Процесс загрузки рюкзака можно разбить на N шагов. На каждом шаге мы решаем вопрос: брать данный предмет или не брать? На каждом шаге имеется всего 2 управления: управление =1, если мы берем данный предмет; и 0 – если не берем.

Состояние системы перед очередным шагом характеризуется весом S, который еще остался в нашем распоряжении до конца полной загрузки после того, как предыдущие шаги выполнены (какие-то предметы уже загружены), т.е. количеством свободного пространства в рюкзаке.

АЛГОРИТМ.

1. Начнем с последнего шага. Сделаем различные предположения о свободном пространстве в рюкзаке: S=0,1,…R. Положим последний предмет в рюкзак, если в нем сводного пространства достаточно.

2. На каждом предыдущем шаге для всех возможных состояний S рассмотрим 2 варианта: брать или не брать предмет. Найдем выигрыш в каждом случае, как сумму выигрышей на текущем шаге и на следующем уже оптимизированном шаге. Результаты занесем во вспомогательную таблицу.

3. На первом шаге рассмотрим только единственно возможное состояние S=R.

4. Найдем решение, «пятясь назад», т.е. взяв оптимальное управление на первом шаге, изменим состояние системы на втором шаге: S=R– x₁ a₁ и выберем оптимальное управление х₂ для этого состояния. И т.д.

ПРИМЕР 4.2.

N=4, R=10

Исходные данные

	П1	П2	П3	П4
вес ai
стоимостьj i

Основная таблица

S	i=4	i=3	i=2	i=1
x4	W4	x3	W3	x2	W2	x1	W1

Вспомогательная таблица.

состояния	x	а	S- а	ji(x)	Wi+1(S- а)	ji(x)+ Wi+1(S- а)
i=3 S=5
S=6
S=7
S=8
S=9
S=10
i=2 S=5
S=6
S=7
S=8
S=9
S=10
i=1 S=10

Ответ: x₄ =0; x₃ =1; x₂ =0; x₁ =1; W=15

ЗАДАЧА 3. О распределении ресурсов.

Имеется N предприятий П₁, П₂,… П_N, каждое из которого дает доход φ_k (x), если ему выделен ресурс в количестве x. Требуется имеющийся в количестве А ресурс распределить между объектами так, чтобы суммарный доход был максимальным.

Пусть x_k – количество ресурса, выделенное k-ому предприятию. Тогда рассматриваемая задача сводится к обычной задаче нелинейного программирования.

Сформулируем задачу, как задачу динамического программирования.

За первый шаг примем вложение средств в предприятие П₁, за второй – в П₂ и т.д. Управляемая система в данном случае – средства, которые распределяются. Состояние системы перед каждым шагом характеризуется одним параметром – наличным запасом еще не вложенных средств. В этой задаче шаговыми управлениями являются средства, выделяемые предприятиям. Требуется найти оптимальное управление (х₁, х₂,…х_N), при котором суммарный доход максимален:

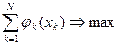
ПРИМЕР 4.3.

N=3 R=5

x	j1(x)	j2(x)	j3(x)
	0,5	0,1
		0,5
	1,5
		2,5

S	i=3	i=2	i=1
x3	W3	x2	W2	x1	W1
				1,1
				3,1		3,5

состояния	x	S-x	ji(x)	Wi+1(S-x)	ji(x)+ Wi+1(S-x)
i=2 S=1			0,1		0,1
S=2			0,1 0,5		1,1 0,5
S=3			0,1 0,5		1,1 1,5
S=4			0,1 0,5		2,1 1,5
S=5			0,1 0,5 2,5		3,1 2,5 2,5
i=1 S=5			0,5 1,5	3,1 1,1	3,1 3,5 2,1 2,6

Ответ: x₁ =1; x₃ =0; x₃ =4; W=3,5

ОБОБЩЕННЫЙ АЛГОРИТМ

1. Описать систему. Т.е выяснить, какими параметрами характеризуется состояние управляемой системы перед каждым шагом. Важно уметь правильно и “скромно” поставить задачу, не переобременяя ее лишними подробностями, упрощая сколько возможно описание управляемой системы.

2. Расчленить операцию на шаги (этапы). Здесь должны быть учтены все разумные ограничения, накладываемые на управление. Шаг должен быть достаточно мелким для того, чтобы процедура оптимизации шагового управления была достаточно проста; и шаг, в то же время должен быть не слишком мелким, чтобы не производить излишних расчетов, усложняющих процедуру поиска оптимального решения, но не приводящих к существенному изменению оптимума целевой функции.

3. Выяснить набор шаговых управлений x_i для каждого шага и налагаемые на них ограничения.

4. Определить, какой выигрыш приносит на i-шаге управление x_i, если перед этим система была в состоянии S, т.е. записать функции выигрыша:

w_i=f_i (S, x_i)

5. Определить, как изменяется состояние системы под влиянием управления x_i на I-м шаге, т.е. записать функции изменения состояния.

S^/=φ_i (S, x_i)

6. Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш через уже известную функцию

W_i (S)= max{f_i (S,x_i)+W_i+1 (φ_i (S, x_i))}

x_i

7. Произвести условную оптимизацию последнего шага, делая различные предположения о том, чем кончился предпоследний шаг, и для каждого из этих предположений найти условное (выбирается исходя из условия, что шаг закончился тем-то) оптимальное управление на последнем шаге.

W_m (S)= max{f_m (S, x_m)}

x_m

8. Произвести условную оптимизацию, начиная с предпоследнего и кончая первым шагом(пятясь назад).

9. Произвести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге: взять найденное оптимальное управление на первом шаге и изменить состояние системы, для найденного состояния найти оптимальное управление на втором шаге и т.д. до последнего шага.

ПРИНЦИП ОПТИМАЛЬНОСТИ. Каково бы ни было состояние системы перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.

Принцип динамического программирования не предполагает, что каждый шаг оптимизируется отдельно, независимо от других. Что толку выбирать управление, эффективность которого максимальна на одном конкретном шаге, если этот шаг лишит нас возможности хорошо выиграть на последующих шагах?

На практике встречаются случаи, когда планировать операцию приходится на неопределенно долгий промежуток времени. Моделью такого случая является бесконечношаговый управляемый процесс, где все шаги равноправны. Здесь функция выигрыша и функция изменения состояния не зависят от номера шага.

Раздел V. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

Дата добавления: 2014-01-20