Решение задач

ЗАДАЧА 6.1. На железнодорожную сортировочную станцию поступает простейший поток составов с интенсивностью λ=2 (состава в час). Обслуживание состава длится в среднем 20 мин. (=1/3 часа).

1) НАЙТИ.

P₀– вероятность того, что система свободна.

L_сист – среднее число составов в районе станции

W_сист – среднее время пребывания составов при станции

L_оч – среднее число составов в очереди

W_оч – среднее время пребывания составов в очереди.

2) Что будет, если время обслуживания увеличится до 30 мин?

3) Сколько должно длиться обслуживание, чтобы время пребывания состава на станции уменьшилось в 2раза?

РЕШЕНИЕ

система 1-канальная с неограниченной очередью

1) µ=1/t_об=3сос./час

ρ= λ/µ=2/3<1

P₀=1- ρ=1/3

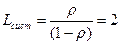
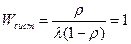
L_оч=

2) µ=1/t_об=2сос./час

ρ= λ/µ=2/2=1 – очередь будет неограниченно расти

3) Wсист=1/2

ЗАДАЧА 6.2. Железнодорожная касса с тремя окошками продаёт билеты в 3 пункта. Интенсивность заявок в пункты одинаковая λ =0.4. Интенсивность обслуживания μ =0,5. На очередь ограничений нет.

1) Найти вероятность того, что придется встать в очередь.

2) Не лучше ли сделать кассы специализированными по продаже билетов только в один пункт?

3) Можно ли ограничиться двумя кассами, продающими билеты во все пункты?

ДАНО.

1) λ1 =0,4 n=3 μ =0,5

2) λ =0,4 n=1 μ =0,5

3) λ =1,2 n=2 μ =0,5

РЕШЕНИЕ.

1) одна трехканальная СМО с неограниченной очередью λ=3* λ₁=1,2

ρ= λ/µ=1,2/0,5=2,4

ρ/3=0,8<1

P₀=(1+ ρ + ρ ²/2+ ρ ³/3!+ρ ⁴/(3!(3- ρ)))^-1 =0,056 P₁=P₀ρ=0,135 P₂=P₀ρ ²/2!=0,162

Вероятность того, что придется встать в очередь P_оч=P₃+ P₄+…=1-(P₀ +P₁+ P₂)=0,65

2) три одноканальные СМО (кассы по одному направлению)

ρ= λ/µ=4/5=0,8<1

Выгоднее использовать кассы по всем направлениям

3) одна двухканальная СМО

ρ= λ/µ=1,2/0,5=2,4

ρ/2=1,2>1 Следовательно, очередь будет неограниченно расти, т.е. 2 кассы для обслуживания потока пассажиров будет недостаточно

ЗАДАЧА 6.3.

АТС имеет 4 канала. На станцию поступают звонки в среднем через каждые 20 секунд (1/3 часа). Вызов, поступивший, когда все линии заняты, получает отказ. Средняя длительность разговора 2 минуты. Найти долю времени, когда все каналы свободны, вероятность отказа, пропускную способность АТС. Сколько должно быть каналов, чтобы вероятность отказа уменьшилась до 20%?

РЕШЕНИЕ

1) 4-канальная система с отказами.

λ=3

µ=1/2=0,5

λ/µ=6

P₀=(1+ ρ + ρ ²/2+ ρ ³/3!+ ρ ⁴/4!)^-1=0,0087

P_отк= P₄=P₀ ·ρ ⁴/4!=0,47

Q =1- p_отк=0,53

А= Q ·λ =0,53 ·3=1,59

2) При n=6

Тогда P₀=(1+ ρ + ρ ²/2+ ρ ³/3!+ ρ ⁴/4!+ ρ ⁵/5!+ ρ ⁶/6!)^-1=0,004

P_отк= P₆=P₀ ·ρ ⁶/6!=0,26

При n=7

Тогда P₀=(1+ ρ + ρ ²/2+ ρ ³/3!+ ρ ⁴/4!+ ρ ⁵/5!+ ρ ⁶/6!+ ρ ⁷/7!)^-1=0,0033

P_отк= P₇=P₀ ·ρ ⁷/7!=0,19

Литература

1. Е.С. Вентцель. Исследование операций. Задачи, принципы, методология. Учеб.пособие для студ.втузов. – М.: Высш.шк., 2001. – 208с.

2. Г.Я. Волошин. Методы оптимизации в экономике. Учебное пособие. – М.: «Издательство «Дело и Сервис», 2004. – 320с.

3. Л.А. Петросян, Г.В. Томский. Через игры к творчеству.–Новосибирск: Наука: Сиб. Отд-ние, 1991.–125с.– (Сер. Наука и технический прогресс»)

4. Ю.М. Ермольцев, И.И. Ляшко, В.С. Михалевич, В.И. Тюптя. Математические методы исследования операций.. Учебное пособие для вузов. – Киев: Вища школа. Головное изд-во, 1979. – 312с.

5. К.А. Рыбников. Введение в комбинаторный анализ.– М.: Изд-во Моск. Ун-та, 1985. – 308с.

6. В.Ф. Капустин. Практические занятия по курсу математического программирования. – Л., Изд-во Ленингр. Ун-та, 1976, – 192с.

7. Ю.И. Рыжиков. Решение научно-технических задач на персональном компьютере. – СПб.: КОРОНА принт, 2000. – 272 с.

8. Ю.В. Васильков, Н.Н. Василькова. Компьютерные технологии вычислений в математическом моделировании: Учеб. Пособие. – М.: Финансы и статистика, 2001. – 256 с.

Дата добавления: 2014-01-20