Определение напряжений и деформаций при раздаче

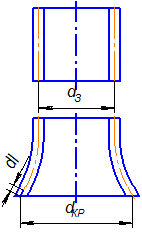
Наиболее просто напряжения и деформации определяются для кромки заготовки

,

,

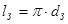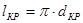тангенсальная деформация.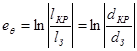

Так как 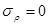, то .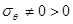

Если считать, что кромка деформируется как модель, близка к линейному растяжению, то для изотропного металла имеет место соотношение следующее соотношение дефомаций

.

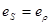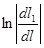– конечная величина.

.

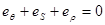
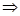
Чтобы определить деформацию для других элементов, используем уравнение связи напряжений и деформаций.

. (*)

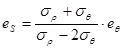Данное уравнение получено из следующего: для монотонного процесса(для немонотонного используют скорости деформаций) имеем:

,

.

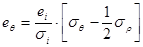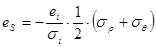Перепишем уравнение (*) в следующем виде:

.

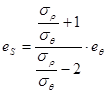Данное уравнение дает возможность определить деформации любого элемента для случая

1. если процесс монотонный, то есть все время происходит либо увеличение, либо уменьшение размеров;

2. когда известна одна из деформаций, например из геометрических соотношений;

3. Соотношение напряжений 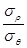находится из условия упрочнения и трения, также как при вытяжке.

Тангенсальную деформацию при раздаче находим из геометрических соотношений. Независимо от того, какой элемент мы рассматриваем с координатой 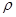– этот элемент имеет длину 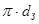. Поэтому для любого элемента мы находим

.

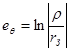Далее определим соотношение напряжений для идеального случая без учета трения, упрочнения, изменения толщины.

Для этот используем инженерный метод, решая уравнение равновесия.

Выделим бесконечно малый элемент.

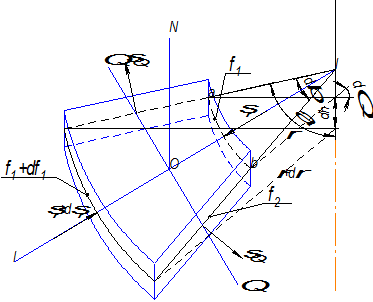
Бесконечно малый элемент находится в равновесии силы, моментов или работы. Так как задача статическая, то мы рассматриваем условие равновесия сил. Находится условие равновесия сил по всем взаимно перпендикулярным осям: , , .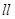

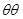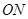В виду симметрии сумма сил на ось 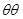обращается в тождество, .

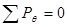Аналогично сумма сил на ось 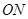обращается в тождество , .

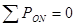Составим уравнение равновесия на ось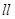

,

,

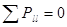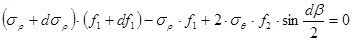здесь ,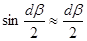

(где S-толщина),

,

,

.

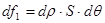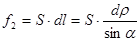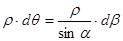После подстановки полученных значений площадей, приравняв слагаемые более высокого порядка к 0, получим:

(**)

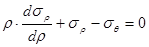напишем упрощенное уравнение пластичности

,

,

,

,

. (***)

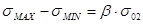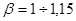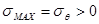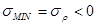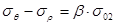После подставки (***) в (**), получим 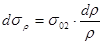- дифференциальное уравнение 1-ого порядка с разделяющимися переменными. После интегрирования последнего выражения, получим

.

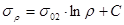Постоянная интегрирования С находится из условия:

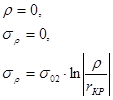
Если провести анализ с учетом трения, то схема действия сил на бесконечно малый элемент будет выглядеть следующим образом:

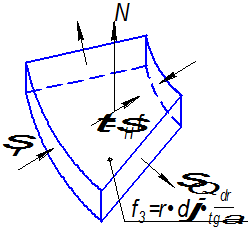
Считаем схему напряженного состояния плоской, но когда учитываем трение, то учитываем касательные напряжения. Напряжение 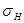суммируется по бесконечной образующей и становится соизмеримым с 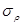и и составляет 30-40%.

,

,

.

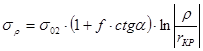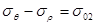Зная эти напряжения, можно построить эпюры.

Дата добавления: 2014-01-20