
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Продолжение Лекции 2. Лекция 3
|
|
|
|
Интерполяционная теорема
Упражнение
Доказать интерполяционную теорему:
Если пропозициональная формула А В – тавтология и формулы
В – тавтология и формулы  А и В не являются тавтологиями, то существует пропозициональная формула С, содержащая только те переменные, которые входят как в А, так и в В, такая, что формулы А
А и В не являются тавтологиями, то существует пропозициональная формула С, содержащая только те переменные, которые входят как в А, так и в В, такая, что формулы А С и С
С и С В суть тавтологии.
В суть тавтологии.
Пояснение:
В определении пропозициональной формулы говорится, что она формируется из пропозициональных переменных, т.е. из переменных, допустимыми значениями которых являются произвольные высказывания. Значит эти переменные в условии теоремы суть пропозициональные переменные, и не могут быть именами, а только высказываниями!
 А – не тавтология. Следовательно, при каких-то переменных
А – не тавтология. Следовательно, при каких-то переменных  А – Л
А – Л 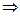 А – И. Хотя при других переменных может быть А – Л.
А – И. Хотя при других переменных может быть А – Л.
В - не тавтология. Следовательно, при каких-то переменных В-Л. Хотя при других переменных может быть В – И.
Итак А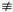 Л (не есть противоречие) и В
Л (не есть противоречие) и В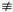 И (не есть тавтология).
И (не есть тавтология).
А В – тавтология. Следовательно, если А – И, то В – И, или, если А – Л, то В – любое.
В – тавтология. Следовательно, если А – И, то В – И, или, если А – Л, то В – любое.
А С – тавтология. Следовательно, если А – И, то С – И, или, если А – Л, то С – любое.
С – тавтология. Следовательно, если А – И, то С – И, или, если А – Л, то С – любое.
С В – тавтология. Следовательно, если С – И, то В – И, или, если С – Л, то В – любое.
В – тавтология. Следовательно, если С – И, то В – И, или, если С – Л, то В – любое.
Отсюда следует, что если А В – тавтология, то чтобы нашлось С, что А
В – тавтология, то чтобы нашлось С, что А С и С
С и С В суть тавтологии, надо, чтобы формулы А, В, С принимали значения:
В суть тавтологии, надо, чтобы формулы А, В, С принимали значения:
А-И, С-И, В-И;
А-Л, С- любое, В- И.
А-Л, С-Л, В-Л.
| А | В | С | А В В
|  А А
| А С С
| С В В
|
| *И | И | И | И | Л | И | И |
| И | И | Л | И | Л | Л | И |
| И | Л | И | Л | Л | И | Л |
| И | Л | Л | Л | Л | Л | И |
| *Л | И | И | И | И | И | И |
| *Л | И | Л | И | И | И | И |
| Л | Л | И | И | И | И | Л |
| *Л | Л | Л | И | И | И | И |
Подходящие варианты отмечены в истинностной таблице звездочками.
 Причем, только для 1-го отмеченного варианта можем утверждать, что
Причем, только для 1-го отмеченного варианта можем утверждать, что  А
А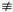 И, т.е. А
И, т.е. А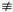 Л,
Л,
и для 4-го отмеченного варианта можем утверждать, что В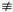 И. Таким образом, чтобы выполнить условие теоремы, формулы для А, В, С должны включать 1-й и 4-й отмеченные звездочкой * варианты, а может и другие из отмеченных вариантов. Т.е., в зависимости от значений входящих в них, т.е. в А, В, С, переменных, истинностная таблица должна давать значения А, В, С, только отмеченные звездочкой, причем 1-й и 4-й отмеченные варианты должны обязательно присутствовать!
И. Таким образом, чтобы выполнить условие теоремы, формулы для А, В, С должны включать 1-й и 4-й отмеченные звездочкой * варианты, а может и другие из отмеченных вариантов. Т.е., в зависимости от значений входящих в них, т.е. в А, В, С, переменных, истинностная таблица должна давать значения А, В, С, только отмеченные звездочкой, причем 1-й и 4-й отмеченные варианты должны обязательно присутствовать!
Итак интерполяционная теорема утверждает, что существует пропозициональная формула С, содержащая только те переменные, которые входят как в А, так и в В, такая, что если формулы А В
В 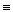 И (есть тавтология), А
И (есть тавтология), А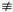 Л и В
Л и В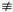 И, то формулы А
И, то формулы А С
С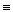 И и С
И и С В
В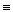 И.
И.
Откуда возникло требование А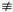 Л, В
Л, В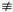 И? Причина, на мой взгляд, следующая. Если А
И? Причина, на мой взгляд, следующая. Если А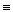 Л, В
Л, В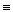 И, то С можно взять любое. В самом деле независимо от значений С – И или Л. А
И, то С можно взять любое. В самом деле независимо от значений С – И или Л. А С и С
С и С В принимает в этом случае значение И. И в этом случае теорема не интересна, т.к. С очевидно существует. Т.е., если С1,…,Сn – переменные входящие в А и В, то в качестве С можно взять любую формулу, зависящую только от С1,…,Сn.
В принимает в этом случае значение И. И в этом случае теорема не интересна, т.к. С очевидно существует. Т.е., если С1,…,Сn – переменные входящие в А и В, то в качестве С можно взять любую формулу, зависящую только от С1,…,Сn.
Доказательство (неверное):
Если в качестве С взять А, то А С равносильно А
С равносильно А А, что есть И (тавтология).
А, что есть И (тавтология).
С В равносильно А
В равносильно А В что по условию теоремы есть тоже И.
В что по условию теоремы есть тоже И.
Аналогично в качестве С можно взять В. Причем нам не понадобились условия А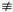 Л и В
Л и В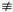 И.
И.
Доказательство неверно, т.к. формула С в этих случаях может содержать переменные, которые входят в А, но не входят в В или наоборот. По условию же теоремы, формула С содержит только те переменные, которые входят как в А, так и в В. Кстати, поэтому видимо теорема и называется интерполяционной. Также, видимо теорема называется интерполяционной еще и потому, что из А В
В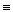 И следуетА
И следуетА С
С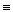 И и С
И и С В
В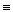 И, т. е. как бы в следование из А формулы В вставили следование через формулу С.
И, т. е. как бы в следование из А формулы В вставили следование через формулу С.
Правильное доказательство:
При доказательстве следует учитывать следующую зависимость формул от переменных Сi, Аj, Вk:
С=С (С1,…,Сn), А=А (С1,…,Сn, А1,…, Аm), В=В (С1,…, Сn, В1,…, В ), А
), А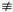 Л, В
Л, В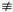 И.
И.
В качестве конкретных значений переменных Сi, Аj, Вk могут подставляться конкретные высказывания, имеющие конкретные истинностные значения И или Л.
Для доказательства теоремы приведем алгоритм, строящий формулу С. Рассуждения, приведшие нас к такому алгоритму, изложены в моей тетради.
1. В качестве С возьмем С= В(С1,…, Сn, В1*,…, В *), где в качестве В1*,…, В
*), где в качестве В1*,…, В * выбираем любые высказывания, т.е. В1*,…, В
* выбираем любые высказывания, т.е. В1*,…, В * могут иметь любые истинностные значения при единственном ограничении: должно быть при данном конкретном наборе С1,…, Сn значение В(С1,…, Сn, В1*,…, В
* могут иметь любые истинностные значения при единственном ограничении: должно быть при данном конкретном наборе С1,…, Сn значение В(С1,…, Сn, В1*,…, В *) иметь значение Л. Следовательно и С будет иметь значение Л. Следовательно, С
*) иметь значение Л. Следовательно и С будет иметь значение Л. Следовательно, С В принимает значение И. Докажем, что А
В принимает значение И. Докажем, что А С принимает значение И.
С принимает значение И.
Действительно А В – И при любом выборе переменных, т.к. по условию теоремы А
В – И при любом выборе переменных, т.к. по условию теоремы А В есть И (тавтология).
В есть И (тавтология).
Отсюда следует, что, так как при заданном выборе С1,…, Сn, есть значения переменных В1,…, В равные В1*,…, В
равные В1*,…, В *, при которых В(С1,…, Сn, В1,…, В
*, при которых В(С1,…, Сn, В1,…, В ) – Л, то А(С1,…,Сn, А1,…, Аm) должно быть Л при заданном выборе С1,…, Сn и выбранных В1*,…, В
) – Л, то А(С1,…,Сn, А1,…, Аm) должно быть Л при заданном выборе С1,…, Сn и выбранных В1*,…, В *. При этом изменение А1,…, Аm не может оказать влияние на значение формулы А. Если мы начнем менять В1,…, В
*. При этом изменение А1,…, Аm не может оказать влияние на значение формулы А. Если мы начнем менять В1,…, В , то А(С1,…,Сn, А1,…, Аm) меняться не будет, т.к. формула А не зависит от В1,…, В
, то А(С1,…,Сn, А1,…, Аm) меняться не будет, т.к. формула А не зависит от В1,…, В . Следовательно А(С1,…,Сn, А1,…, Аm) будет Л при любых В1,…, В
. Следовательно А(С1,…,Сn, А1,…, Аm) будет Л при любых В1,…, В . Итак при заданном выборе С1,…, Сn, формула А=А(С1,…,Сn, А1,…, Аm) будет Л при любых В1,…, В
. Итак при заданном выборе С1,…, Сn, формула А=А(С1,…,Сn, А1,…, Аm) будет Л при любых В1,…, В и А1,…, Аm.
и А1,…, Аm.
Итак мы получили, что при заданном выборе С1,…, Сn, формулы А, С принимают значения Л. При этом значение В может быть любым. Следовательно, А С – И и С
С – И и С В – И.
В – И.
2. Если же при данном конкретном наборе С1,…, Сn нет ни одного набора В1,…, В , что В будет иметь значение Л, т.е. В(С1,…, Сn, В1,…, В
, что В будет иметь значение Л, т.е. В(С1,…, Сn, В1,…, В ) имеет значения И при любых В1,…, В
) имеет значения И при любых В1,…, В , то берем в качестве С(С1,…, Сn) значения В(С1,…, Сn, В1,…, В
, то берем в качестве С(С1,…, Сn) значения В(С1,…, Сn, В1,…, В ), где В1,…, В
), где В1,…, В принимают любые значения без ограничений. В этом случае В принимает значения И. Следовательно С – тоже И. Так как по условию теоремы А
принимают любые значения без ограничений. В этом случае В принимает значения И. Следовательно С – тоже И. Так как по условию теоремы А В есть И, а, как только что установили, В – И, то следовательно А может быть и Л и И. Значит А
В есть И, а, как только что установили, В – И, то следовательно А может быть и Л и И. Значит А С и С
С и С В есть И.
В есть И.
Итак, мы построили С и, следовательно, доказали интерполяционную теорему.
Упражнение на дом.
Доказать, что в качестве С в интерполяционной теореме, при заданном выборе С1,…, Сn, можно взять:
1) А(С1,…,Сn, А1*,…, Аm*), если оно имеет значение И и
2) А(С1,…,Сn, А1,…, Аm), если значение А – Л, при любом А1,…, Аm. Тогда надо при выбранном С1,…, Сn взять любое А1,…, Аm.
Возникает вопрос является ли так заданная С формулой. Действительно, мы имеем для любых вариантов задания значений С1,…, Сn какое-то значение выражения С(С1,…, Сn), значение которого И или Л. Так как вариантов значений С1,…, Сn 2n и на каждый приходится 2 возможных значения С, равных И или Л, следовательно, максимальное число функций  . Причем мы не различаем между собой функции, отличающиеся видом связи переменных, если они имеют одинаковое истинностное значение (пример, Р1
. Причем мы не различаем между собой функции, отличающиеся видом связи переменных, если они имеют одинаковое истинностное значение (пример, Р1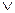 Р1 и Р1&Р1). Оказывается (мы докажем в дальнейшем для функции двух переменных), что все эти
Р1 и Р1&Р1). Оказывается (мы докажем в дальнейшем для функции двух переменных), что все эти  различных функций от переменных С1,…, Сn можно выразить виде формул, куда входят С1,…, Сn и логические связки. Отметим, что описанный алгоритм обязательно даст какую-то функцию С(С1,…, Сn), может быть и не одну. Отметим также, что мы нигде не использовали требования А
различных функций от переменных С1,…, Сn можно выразить виде формул, куда входят С1,…, Сn и логические связки. Отметим, что описанный алгоритм обязательно даст какую-то функцию С(С1,…, Сn), может быть и не одну. Отметим также, что мы нигде не использовали требования А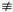 Л, В
Л, В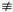 И. Тогда откуда возникло это требование? Причина, на мой взгляд, следующая. Если А
И. Тогда откуда возникло это требование? Причина, на мой взгляд, следующая. Если А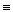 Л, В
Л, В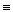 И, то С можно взять любое, т.е. в качестве С (С1,…, Сn) можно взять любую из
И, то С можно взять любое, т.е. в качестве С (С1,…, Сn) можно взять любую из  функций. В самом деле независимо от значений С – И или Л. А
функций. В самом деле независимо от значений С – И или Л. А С и С
С и С В принимает в этом случае значение И.
В принимает в этом случае значение И.
И в этом случае теорема не интересна, т.к. С очевидно существует.
Практика 2
Высказывания и высказывательные формы. Истинностные таблицы.
Приведем условие простейшей задачи №5 из билета №1 первой контрольной, относящуюся к интерполяционной теореме:
Для A=C1ÙA1, B=B1®C1 (проверить, что A®B= И), найти C=С(С1), что A®C= И, C®B= И.
Эта и другие более сложные задачи придумывались и решались следующим образом (полный текст с решениями всех задач в тетради).
Интерполяционная теорема
Если A®B= И, А¹ Л, В¹ И.
А=А(С1,…,Сn, А1,…, Аm), В=В(С1,…, Сn, В1,…, В ), то
), то
существует С=С(С1,…, Сn), что формулы А®С= И, С®В= И.
Задачи будут придумываться так:
Для выбранных n, m, l буду строить таблицы истинности для A, B, удовлетворяющих условию задачи. Потом по следующему алгоритму, буду находить таблицу истинности для C. Алгоритм (в квадратных скобках красным цветом показан другой вариант алгоритма):
1) Перебираем таблицу истинности для С, A, B. Значения С еще не заполнены.
2) Находим строки в которых В(С1,…, Сn, В1*,…, В *)=Л [А(С1,…,Сn, А1*,…, Аm*)=И].
*)=Л [А(С1,…,Сn, А1*,…, Аm*)=И].
Если для С1,…, Сn такие строки есть, то задаем для таких С1,…, Сn
С(С1,…, Сn)=Л [С(С1,…, Сn)=И].
3) Для С1,…, Сn, для которых нет ни при каких В1,…, В [А1,…, Аm] значений
[А1,…, Аm] значений
В(С1,…, Сn, В1,…, В )=Л [А(С1,…,Сn, А1,…, Аm)=И], т.е. при любых В1,…, В
)=Л [А(С1,…,Сn, А1,…, Аm)=И], т.е. при любых В1,…, В [А1,…, Аm] для данных С1,…, Сn В(С1,…, Сn, В1,…, В
[А1,…, Аm] для данных С1,…, Сn В(С1,…, Сn, В1,…, В )=И [А(С1,…,Сn, А1,…, Аm)=Л], то и С(С1,…, Сn)=И [С(С1,…, Сn)=Л]задаем.
)=И [А(С1,…,Сn, А1,…, Аm)=Л], то и С(С1,…, Сn)=И [С(С1,…, Сn)=Л]задаем.
Я, для A, B. С, а студенты для С по таблицам истинности строят СДНФ (совершенную дизъюнктивную нормальную форму) так, как изложено в лекции 6.
Задачу формулирую так:
Для данных А, В (заданных формулами), проверить, что A®B= И. Найти С(С1,…, Сn). Сначала таблицу истинности, а потом СДНФ, что А®С= И, С®В= И.
Итак:
1-ый вариант.
| С1 | А1 | В1 | ¹Л А | ¹И В | =И A®B | С | =И А®С | =И С®В |
| 1 | 1 [1] | 1 | 1[1] | |||||
| 1 | 1 [1] | 1 | 1[1] | |||||
| 1 | 0 [0] | 1 | 1[1] | |||||
| 1 | 0 [0] | 1 | 1[1] | |||||
| 0 | 0 [ 0 ] | 0 | 0 [ 0 ] | |||||
| 0 [ 0 ] | 0 [ 0 ] | |||||||
| 0 [ 0 ] | 0 [ 0 ] | |||||||
| 0 [ 0 ] | 0 [ 0 ] |
СДНФ: A= С11∧ A11= С1 ∧ A1


 B= (С11∧ B11) ∨(С11∧ B10) ∨(С10∧ B10)= (С1∧ B1) ∨(С1∧ B1) ∨(С1∧ B1)=
B= (С11∧ B11) ∨(С11∧ B10) ∨(С10∧ B10)= (С1∧ B1) ∨(С1∧ B1) ∨(С1∧ B1)=







 =(С1∧ (B1 ∨ B1) ∨(С1∧ B1)= (С1 ∨(С1∧ B1)= (С1∨ С1) ∧ (С1∨ B1)= С1∨ B1= B1®С1.
=(С1∧ (B1 ∨ B1) ∨(С1∧ B1)= (С1 ∨(С1∧ B1)= (С1∨ С1) ∧ (С1∨ B1)= С1∨ B1= B1®С1.
C=С11=С1.
Итак задача: Для A=C1ÙA1, B=B1®C1 (проверить, что A®B= И), найти C=С(С1), что A®C= И, C®B= И.
0-ой вариант.
| С1 | С2 | А1 | В1 | ¹Л А | ¹И В | =И A®B | С | =И А®С | =И С®В |
| 1 [ 1 ] | 1 | 1 [ 1 ] | |||||||
| 1 [1] | 1 | 1 [ 1 ] | |||||||
| 1 [1] | 1 | 1 [ 1 ] | |||||||
| 1 [1] | 1 | 1 [ 1 ] | |||||||
| 1 [ 1 ] | 1 | 1 [ 1 ] | |||||||
| 1 [1] | 1 | 1 [ 1 ] | |||||||
| 0 [0] | 1 | 1 [ 1 ] | |||||||
| 0 [0] | 1 | 1 [ 1 ] | |||||||
| 0 [ 0 ] | 0 | 0 [ 0 ] | |||||||
| 0 [ 0 ] | 0 [ 0 ] | ||||||||
| 0 [ 0 ] | 0 [ 0 ] | ||||||||
| 0 [ 0 ] | 0 [ 0 ] | ||||||||
| 0 [0] | 1 | 1 [ 1 ] | |||||||
| 0 [0] | 1 | 1 [ 1 ] | |||||||
| 1 [ 1 ] | 1 | 1 [ 1 ] | |||||||
| 1 [1] | 1 | 1 [ 1 ] |
СДНФ: A= (С11∧С21∧ A11) ∨(С11∧С21∧ A10) ∨(С11∧С20∧ A11) ∨(С10∧С20∧ A10) =
= (С1∧С2∧ A1) ∨(С1∧С2∧ ØA1) ∨(С1∧ØС2∧ A1) ∨(ØС1∧ØС2∧ØA1)=
= ((С1∧С2)∧ (A1 ∨ ØA1)) ∨(С1∧ØС2∧ A1) ∨(ØС1∧ØС2∧ØA1)=
= (С1∧С2) ∨(С1∧ØС2∧ A1) ∨(ØС1∧ØС2∧ØA1)= (С1∧(С2 ∨(ØС2∧ A1))) ∨(ØС1∧ØС2∧ØA1)=
= (С1∧((С2 ∨ØС2)∧(С2 ∨A1))) ∨(ØС1∧ØС2∧ØA1)= (С1∧(С2 ∨A1)) ∨(ØС1∧ØС2∧ØA1)=
= (С1∧(С2 ∨A1)) ∨(ØС1∧Ø(С2∨A1))=С1 «(С2∨ A1)
B= (С11∧С21∧B11) ∨(С11∧С21∧B10) ∨(С11∧С20∧B11) ∨(С11∧С20∧B10) ∨
∨ (С10∧С21∧B10) ∨(С10∧С20∧B11) ∨ (С10∧С20∧B10) =
= (С1∧С2∧B1) ∨(С1∧С2∧ØB1) ∨(С1∧ØС2∧B1) ∨(С1∧ØС2∧ØB1) ∨
∨ (ØС1∧С2∧ØB1) ∨(ØС1∧ØС2∧B1) ∨ (ØС1∧ØС2∧ØB1) =
= (С1∧С2) ∨(С1∧ØС2) ∨ (ØС1∧С2∧ØB1) ∨(ØС1∧ØС2) =
= С1 ∨ (ØС1∧((С2∧ØB1) ∨ØС2) = С1 ∨ (ØС1∧(С2∨ØС2)∧(ØB1 ∨ØС2)) =
= С1 ∨ (ØС1∧(ØB1 ∨ØС2)) = (С1 ∨ ØС1)∧(С1 ∨(ØB1 ∨ØС2)) = C1ÚØC2ÚØB1.
C= (С11∧С21) ∨(С11∧С20) ∨(С10∧С20) = (С1∧С2) ∨(С1∧ØС2) ∨(ØС1∧ØС2) =
= (С1∧(С2 ∨ØС2)) ∨(ØС1∧ØС2) = С1 ∨(ØС1∧ØС2) = (С1 ∨ØС1)∧ (С1 ∨ØС2) =
=С1∨ØС2.= С2® С1.
Итак задача: Для A= С1 «(С2∨ A1), B= C1ÚØC2ÚØB1 (проверить, что A®B= И), найти C=С(С1,C2), что A®C= И, C®B= И.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 419; Нарушение авторских прав?; Мы поможем в написании вашей работы!