Лекция 6. Рассмотрим двухэлементное множество В, элементы которого обозначим 0 и 1

Логические функции.

Рассмотрим двухэлементное множество В, элементы которого обозначим 0 и 1. Причем будем иметь в виду, что здесь 0 и 1 не являются числами в обычном смысле, хотя по некоторым свойствам и похожи на них. Наиболее распространенная интерпретация двоичных переменных «1», «0» — логическая: это «ДА», «НЕТ», или «истинно», «ложно», или «Т», «F».

Как мы уже видели можно выбрать n - переменных (х₁, х₂,..., х_n), каждая из которых принимает значения из двухэлементного множества {0, 1}, и построить двоичную функцию f(х₁, х₂,..., х_n).

Логическая функция f (х₁, х₂,..., х_n) — это функция, принимающая значения на двоичном множестве В.

Множество всех логических функций принято обозначать Р₂;

Множество всех двоичных функций от «n» переменных — Р₂ (n).

Всякая логическая функция «n» переменных может быть задана таблицей, в левой части которой перечислены все 2ⁿ наборов значений переменных (то есть всевозможных наборов двоичных векторов длины «n»), а в правой части приведены значения функции на этих наборах. Например, для функции f (х₁, х₂, х₃), таблица будет:

х1	х2	х3	f

При любом фиксированном упорядочении наборов значений переменных логическая функция «n» переменных полностью определена вектор - столбцом своих значений, то есть вектором длины 2ⁿ. Поэтому число различных логических функций «n» переменных будет

. В самом деле, для одного набора значений своих переменных (строка левой части таблицы) значение функции может быть либо 1, либо 0 (две возможности). Число же возможных различных наборов аргументов функции, как уже отмечалось равно 2ⁿ,

поэтому число различных логических функций будет .

Например, если n = 1, то возможны четыре различные логические функции от одной переменной, они приведены в таблице 2.

Таблица 2.

X	ψ0 ψ1 ψ2 ψ3 φ3
	0 0 1 1 0 1 0 1 11

Функции ψ ₀, ψ ₃ - константы 0 и 1 соответственно; их значения не зависят от значений переменных, и, следовательно значения переменной х для них несущественны. Значения функции ψ ₁(х) «повторяют» значения х: ψ ₁ (x)= х. Функция ψ ₂(х) называется отрицанием «х» (или функцией НЕ) и обозначается: ¬x, х, ~ х. Ее значение противоположно значению «х».

Число логических функций двух переменных - 16; они приведены в таблице 3.

Таблица 3.

Х1

Х2

ψ 0

ψ 1

ψ 2

ψ 3

ψ 4

ψ 5

ψ 6

ψ 7

ψ 8

ψ 9

ψ 10

ψ 11

ψ 12

ψ 13

ψ 14

ψ 15

Функции ψ ₀и ψ ₁₅ константы 0 и 1, то есть функции с двумя несущественными переменными.

Функция ψ ₁ (x₁, x₂) называется конъюнкцией x₁и х₂; обозначают такие функции так: x₁ & х₂, или x₁ ∧ x₂, или x_{1 *} x₂. Функция конъюнкции равна 1, только в том случае, если x₁ и х₂ одновременно равны 1, поэтому часто функцию конъюнкции называют функцией «И». Еще одно название функции конъюнкции — это «логическое умножение», поскольку ее таблица действительно совпадает с таблицей умножения для чисел 0 и 1.

Функция ψ₇ (x₁, x₂) называется дизъюнкцией x₁ и х₂; ее обозначают: x₁ ∨ x₂, или x₁+ х₂. Она равна 1, если x₁ или х₂ равны 1. Часто эту функцию называют функцией «ИЛИ» (здесь «или» понимается в неразделительном смысле - хотя бы одно из двух). Еще одно название – логическое сложение.

Функция ψ₆ (x₁, x₂) - функция сложения по модулю 2. Ее обозначают: x₁ ⊕ х₂, или x₁ ∆ х₂ (а мы вводили как x₁ ∨ х₂). Она равна 1, когда значения ее аргументов различны, и равна 0, когда значения ее аргументов равны. Поэтому функцию ψ₆ (x₁, x₂) иногда называют функцией неравнозначности.

Функция ψ₉ (x₁, x₂) называется эквивалентностью, или равнозначностью. Ее обозначают x₁ ~ х₂, или x₁ ≡ х₂ (вместо ~ и ≡ мы используем ↔ и Û, а так ≡ мы задавали логическую эквивалентность двух выражений). Она равна 1, когда значения ее аргументов равны, и функция равна 0, когда значения ее аргументов различны.

Еще три функции имеют свои названия:

ψ₁₃ (x₁, x₂) - импликация; обозначения: x₁ → х₂, или x₁ ⊃ х₂; читается: «если x₁, то х₂»;

ψ₈ (x₁, x₂) - "стрелка Пирса"; обозначение: x₁↓х₂ ≡ x₁ ∨ х₂.

ψ₁₄ (x₁, x₂) - "штрих Шеффера"; обозначение: x₁ | х₂ ≡ x₁ & х₂.

Остальные функции специальных названий не имеют и легко выражаются через перечисленные ранее функции.

Отметим, что для функций ψ₃ и ψ₁₂ – переменная х₂ – фиктивна, т. е. никак не влияет на значение функции и ее можно просто удалить, что никак не отразится на функции. Из таблицы 3 мы видим, что ψ₃ (x₁, x₂) = x₁, и ψ₁₂ (x₁, x₂) = x₁.

Для функций ψ₅ и ψ₁₀ фиктивной является переменная x_1. В самом деле, ψ₅ (x₁, x₂) =

х₂, ψ₁₀ (x₁, x₂) = х₂.

Таким образом, из 16 функций двух переменных шесть функций имеют фиктивные переменные. С ростом числа переменных доля функций, имеющих фиктивные переменные убывает и стремится к нулю.

Суперпозиции функций и формулы.

Суперпозиция функций имеет место, когда аргументом функции оказывается функция. При этом формулой мы называем выражение, которое описывает такую суперпозицию функций.

Например:

(х₃ ∨ x₁) ⊕ (x₁ & (x₁ ⊕ x₂)) описывает суперпозицию функций: f₃ (f₁(х₃, x₁), f₂ (x₁, f₃ (x₁, x₂))), где f₁ (a, b) = (a ∨ b); f₂ (a, b) = (a & b); f ₃ (a, b) = (a ⊕ b).

Понятно, что формула каждому набору значений аргументов ставит в соответствие значение функции и, следовательно, может служить наряду с таблицей способом задания и вычисления функции. О формуле задающей функцию, говорят также, что она реализует или представляет эту функцию.

В отличие от табличного задания представление данной функции формулой не единственно. Например, если в качестве исходного множества функций зафиксировать множество функции «И», «ИЛИ», «НЕ», то функцию штрих Шеффера можно представить формулами:

(x₁ | x₂) ≡ (x₁ ∨ x₂) ≡ (x₁& x₂), а функцию стрелка Пирса можно представить формулами:

(x₁↓x₂)≡(x₁& x₂) ≡ (x₁∨ x₂)

Формулы, представляющие одну и ту же функцию, называются эквивалентными или равносильными.

Совершенная дизъюнктивная нормальная форма логической функции

Как отмечалось выше, на множестве высказываний определено 4 бинарные операции. Кроме них существуют и другие. Все они участвуют в определениях различных логических функций, которые в некоторых случаях принимают весьма сложный вид. Формулы (1) позволяют выражать импликацию и эквивалентность через дизъюнкцию и конъюнкцию.

a ® b =Ø a Ú b,

a ~ b =(Ø a Ú b)Ù(a ÚØ b) (1)

Возникает естественный вопрос: «можно ли любую логическую функцию представить с помощью отрицания, конъюнкции и дизъюнкции?» Ответ на него дает следующее утверждение, которое мы приведем без доказательства.

Теорема. Всякая логическая функция может быть представлена аналитической формулой, содержащей конечное число операций отрицания, дизъюнкций и конъюнкций.

Для построения такой формулы вводится функция х^σ, принимающая два значения при разных истинностях логического параметра σ:

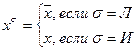(2)

Следует специально отметить, что σ - не является показателем степени, а х^σ - степенной функцией. Запись этой логической функции условна, а использовать ее можно только в смысле, определенном формулой (2).

Оказывается, для любой логической функции f(x _1, ..., x_n), не являющейся тождественно ложной, справедливо равенство

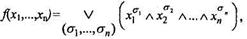
(3)

где логическое суммирование производится перебором всех булевых значений, И и Л, высказываний σ _i (i =1,…, n) для которых f( σ_1, ..., σ _n) = И. Записанная формула называется разложением функции по переменным, или совершенной дизъюнктивной нормальной формой (д.н.ф.) ее.

Пример. Пусть функция y = f(x_1, x_2, x_3,) задана следующей таблицей истинности.

N	x1	х2	x3	f(x1, x2, x3,)
	Л	Л	Л	И
	Л	Л	И	И
	Л	И	Л	Л
	Л	И	И	Л
	И	Л	Л	Л
	И	Л	И	И
	И	И	Л	Л
	И	И	И	И

Очевидно, что f( σ_1, σ_2, σ₃) = И для тех значений параметров σ_1, σ_2, σ_3, которые совпадают со значениями аргументов x_1, x_2, x₃, расположенными в строках под номерами 0, 1, 5, и 7. В них тройки параметров имеют значения (Л,Л,Л), (Л,Л,И), (И,Л,И) и (И,И,И). Следовательно, согласно формуле (3), мы имеем:

Таким образом, из определения х^σ, т.е. из формулы (2), окончательно получается совершенная дизъюнктивная нормальная форма данной функции:

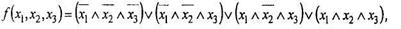
которая представляет данную в таблице функцию трех переменных в виде совокупности операций логического сложения, умножения и отрицания ее аргументов. Кстати, легко заметить, что сгруппировав первые две и последние два логических слагаемых, получим для данного примера f(x₁, x₂, x₃)= (Øx₁∧Øx₂) ∨ (x₁∧x₃).

Дата добавления: 2014-01-20