Распределение Максвелла молекул по скоростям

Представим себе сосуд с газом, помещенный в пустое пространство. Газ внутри сосуда находится в равновесии и его молекулы каким-то образом распределены по скоростям. Это распределение нам и требуется найти. Рассмотрим движение молекулы вдоль оси ОХ. Можно доказать, что вероятность того, что скорость центра масс любой молекулы лежит в интервале от v_x до v_x + dv_x (мы опускаем индекс "О" для скорости центра масс), определяется выражением:

В предыдущих лекциях мы уже неоднократно
использовали понятия средних значений
различных физических величин,

характеризующих движение молекул: среднюю скорость, среднюю кинетическую энергию поступательного движения молекулы и т.д.

Нетрудно видеть, что средние значения физических величин тоже тесно связаны с понятием вероятности.

Пусть требуется определить некоторую величину а, относящуюся к какой-либо системе частиц. Для этого мы должны проделать (конечно, мысленно) множество наблюдений над системой (их число равно N). Тогда окажется, что при Nj наблюдениях мы найдем, что интересующая нас величина а имеет значение а^ N₂ наблюдений дадут для а значение а₂ и т.д. Среднее значение а, по определению, равно:

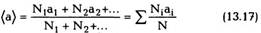
Это означает, что число молекул, находящихся в тепловом равновесии при температуре Т и обладающих скоростью v_x в интервале от v_x до v_x + dv_x равно

Постоянную А можно определить из условия, что

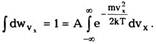
Делая замену переменных

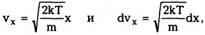
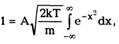
получим

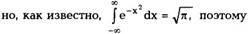
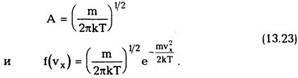
Рассмотрим теперь случай, когда случайная величина а может принимать не дискретные значения а_р а₂,..... а любые. В этом случае задача ставится следующим образом. Какова вероятность того, что случайная величина а при измерении будет иметь значение от а до a + da, где da — бесконечно малое изменение а? Можно записать, что эта вероятность

случайной величины а, или ее функцией распределения. Среднее значение величины а определяется тогда по формуле

где интегрирование проводится по всем возможным значениям величины а. При этом

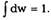
Полученное выражение для функции распределения молекул по х-компонентам скоростей не может быть "привилегией" именно х-компоненты скорости. Очевидно, что совершенно такие же выражения должны определять и распределения молекул по другим компонентам скорости, так что

Теперь мы можем найти вероятность того, что скорость любой молекулы удовлетворяет одновременно трем условиям:

Это означает, что число таких молекул

Дата добавления: 2014-01-20