Показатели безотказности

Вероятность безотказной работы P(t) есть вероятность того, что в пределах заданной наработки отказ объекта не возникает. Стати­стически вероятность безотказной работы можно определить отноше­нием числа объектов, безотказно проработавших до момента времени t, к числу объектов, работоспособных в начальный момент времени.

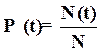, (2.1)

где N(t) — число объектов, безотказно проработавших до момента времени t; N - число объектов, взятых под наблюдение.

В начальный момент времени (перед испытаниями) все объекты являются исправными, т. е. выполняется равенство N(t) = N, P(t) = 1.

Если испытания проводятся до отказа всех N объектов, то в конце испытаний N (t) = 0; P(t) = 0.

Следовательно, вероятность безотказной работы в течение конечных интервалов времени может иметь значения 0 P(t) 1.

Из теории вероятностей следует, что вероятность суммы двух несовместимых противоположных событий равна единице.

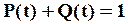, (2.2)

где Q(t) — вероятность отказа.

Отсюда:

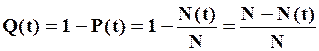, (2.3)

где N - N(t) — число отказавших объектов к моменту времени t.

С увеличением наработки вероятность безотказной работы уменьшается, а вероятность отказа возрастает. На рис. 2.1 оба графика характеризуют распределение случайного времени безотказной работы. Однако кривая Q(t) показывает вероятность того, что в течение времени t отказ наступит, а кривая P(t) позволяет найти вероятность того, что отказа за время t не произойдет.

Средняя наработка до отказа есть математическое ожидание наработки объекта до первого отказа.

Статистически средняя наработка до отказа определя­ется отношением суммы нара­ботки испытуемых объектов до отказа к числу наблюдаемых объектов, если они все отказали за время испытаний.

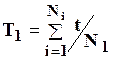, (2.4)

где ti — наработка i-го объекта до первого отказа; N1 — число отказавших объектов.

Оценка средней наработки до отказа зависит от плана ис­пы­таний и закона распределе­ния наработки до отказа.

	Интенсивность отка­зов есть условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рас­смат­ри­ваемого момента вре­мени, при условии, что до этого момента отказ не возник. Плотность вероятно­сти отказа в момент t — пре­дел отноше­ния вероятности от­каза в интервале времени от t до (t + t) к величине интервалаt при t 0. Физический смысл
Рис. 2.1. Изменение вероятности без­отказной работы P(t) и вероятности появления отказов Q(t) от наработки t.	плотности вероятности отказа — это вероятность отказа в доста­точно малую единицу времени.

Из определения интенсивности отказов (t):

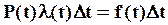, (2.5)

где f(t) — плотность распределения наработки до отказа.

Из этого соотношения:

. (2.6)

Статистически интенсивность отказов определяется отношением разности между числом отказов r(t + t) на момент времени (t + t) и числом отказов r(t) на момент времени t к длительности интервала времени t

. (2.7)

Параметр потоков отказов (t) есть плотность вероятности возникновения отказов восстанавливаемого объекта, определяемая для рассматриваемого момента времени.

Рассмотрим эксплуатацию восстанавливаемых объектов. В начальный момент времени изделие начинает работу и работает до отказа. При отказе происходит восстановление объекта, и он вновь работает до отказа и т. д. Моменты отказов формируют поток отказов. В качестве характеристики потока отказов используют математическое ожидание числа отказов W (t) за время t.

. (2.8)

Математическое ожидание числа отказов за интервал времени (t₁, t₂) определяют по формуле:

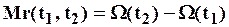, (2.9)

где r(t₁, t₂) — число отказов за интервал времени (t₁, t₂).

Функция:

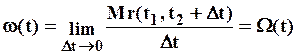(2.10)

называется интенсивностью потока отказов.

При экспоненциальном законе распределения наработки между отказами:

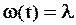. (2.11)

Наработка на отказ есть отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Статистически наработка на отказ определяется отношением суммарной наработки восстанавливаемых объектов к суммарному числу отказов этих объектов:

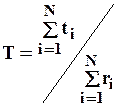, (2.12)

где ti — наработка i-го объекта за период наблюдений; ri — число отказов i-го объекта за период наблюдений.

Дата добавления: 2014-01-20