Методы дискретной математики

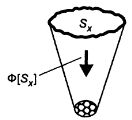Теоретико-множественные представления. Базируются на понятиях «множество», «элементы множества», «отношения на множествах».

Символическое представление системы в виде множества, состоящего из совокупности подмножеств, представлено на рисунке слева.

Понятие «множество» относится к числу интуитивно постигаемых понятий, которым трудно дать определение. Это понятие содержательно эквивалентно понятиям «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «класс» и другим обобщающим понятиям.

Один из основоположников теории множеств Георг Кантор определял множество как «многое, мыслимое нами как единое».

Множества могут задаваться следующими способами:

1) списком, перечислением (интенсионально); например,

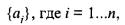
или

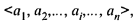
где a_iÎА; Î — знак вхождения элементов в множество;

2) путем указания некоторого характеристического свойства А (экстенсионально). Например, «множество натуральных чисел», «множество рабочих данного завода», «множество планет солнечной системы», «множество А» и т. д.

В основе теоретико-множественных преобразований лежит принцип перехода от одного способа задания множества к другому:

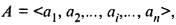
или

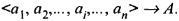
Переход от интенсионального способа задания множества к экстенсиональному называют принципом свертывания.

В множестве могут быть выделены подмножества. Вхождение элементов в любое множество или подмножество описывается знаком «принадлежит» — Î, а вхождение подмножества в множество записывается так: ВÌA.

Это означает, что все элементы подмножества В являются одновременно элементами множества А (рис. 7.2):

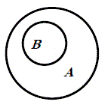
Рис. 7.2

Важным понятием является понятие «пустого множества» — множества, в котором в данный момент нет ни одного элемента: D = Æ.

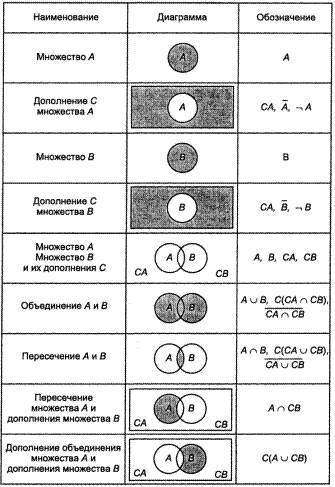
При использовании теоретико-множественных представлений в соответствии с концепцией Кантора можно вводить любые отношения. При уточнении этих отношений применительно к множествам удобно пользоваться наглядными диаграммами Эйлера-Венна. Примеры таких диаграмм для операции объединения (È), пересечения (& или Ç), дополнения (отрицания, обозначаемого знаком «—» над именем множества, либо знаком «Ø,» перед именем множества или его элемента) приведены в табл. 7.2.

Математическая логика. Логические представление переводят реальную систему и отношения в ней на язык из одной из алгебр логики (двузначной, многозначной), основанной на применении алгебраических методов для выражения законов алгебры логики.

Базовыми понятиями математической логики являются высказывание, предикат, логические функции (операции) кванторы, логический базис, логические законы (законы алгебры логики).

Под высказыванием в алгебре логики понимается повествовательное предложение (суждение), которое характеризуется определенным значением истинности.

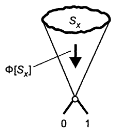
В простейших случаях используется два значения истинности: «истинно»-«ложно», «да»-«нет», «1»-«0». Такая алгебра логики, в которой переменная может принимать только два значения истинности, называется бинарной алгеброй логики Буля (по имени ее создателя).

Символическое отображение системы в параметрах бинарной логики представлено на рисунке слева.

Табл. 7.2

Дата добавления: 2014-01-20