Тест - контроль для самопроверки. Выход темы в другие темы и дисциплины

Выход темы в другие темы и дисциплины

Данная тема имеет выход в дипломные, магистерские и диссертационные работы.

4.1. Линеаризацией нелинейной задачи называется

А. Следующая последовательность процедур:

1. Проверка выполнения условий применения данной итерационной схемы.

2. Разделение корней (выделение подобластей, включающих единственный корень) и выбор нулевых приближений для каждой подобласти..

3. Выполнение итераций, включающих

- формулирование линейной задачи 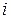- ой итерации;

- решение этой задачи с использованием результатов предыдущей итерации (предыдущих итераций);

- проверка условий выхода из итерационного цикла;

- при выполнении указанных условий – выход из цикла.

Б. Формулирование линейной задачи 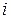- ой итерации.

В. Формулирование и решение линейной задачи 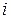- ой итерации с использованием результатов предыдущей итерации (предыдущих итераций).

Г. Преобразование нелинейной задачи в линейную задачу.

4.2. Неподвижной точкой оператора называется

А. Наименьшее из таких чисел 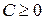, для которых выполняется условие

,

где 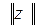и 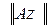- нормы элемента 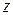и его образа .

Б. Элемент 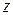, удовлетворяющий условию 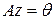, где 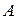- заданный оператор, 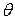- нулевой элемент.

В. Элемент 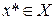, удовлетворяющий условию .

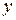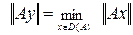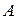Г. Элемент .такой, что , где - заданный оператор.

4.3. Область сходимости неподвижной точки оператора 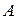- это

А. Область , если для каждой точки 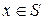существует элемент .

Б. Область , если для каждой точки можно указать такой элемент 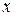, что .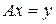

В. Множество всех элементов 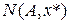такое, что для любого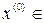 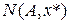последовательность 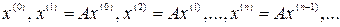принадлежит ей.

Г. Множество всех элементов 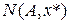такое, что для любого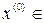 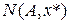последовательность 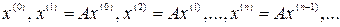сходится к .

4.4. Оператором сжатия называется

А. Оператор 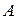, удовлетворяющий условию , где - нулевой элемент.

Б. Оператор 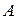, удовлетворяющий условию , если .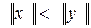

В. Оператор , для которого можно указать постоянную 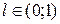такую, что .

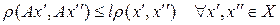Г. Оператор , для которого можно указать постоянную такую, что .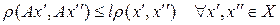

4.5. Методом простых итераций называется

А. Следующая последовательность вычислительных процедур.

1. Проверка возможности использования метода.

2. Выбор начальной точки.

3. Последовательное выполнение итераций, причём любая 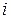- ая итерация выполняется по формуле .

4. Условия выхода из цикла могут иметь следующий вид:

,

,

.

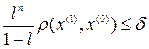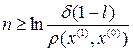Б. Следующая последовательность вычислительных процедур:

1. Проверка возможности использования метода.

2. Выбор начальной точки.

3. Последовательное выполнение итераций, причём любая 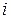- ая итерация выполняется по формуле .

4. Условия выхода из цикла могут иметь следующий вид:

,

,

.

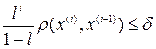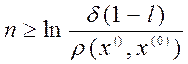В. Следующая последовательность вычислительных процедур:

1. Проверка возможности использования метода.

2. Выбор начальной точки.

3. Последовательное выполнение итераций, причём любая 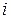- ая итерация выполняется по формуле .

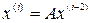4. Условия выхода из цикла могут иметь следующий вид:

,

,

.

Г. Следующая последовательность вычислительных процедур:

1. Проверка возможности использования метода.

2. Выбор начальной точки.

3. Последовательное выполнение итераций, причём любая - ая итерация выполняется по формуле .

4. Условия выхода из цикла могут иметь следующий вид:

,

,

.

Ответы на тест – самоконтроль 4.5 (Адрес файла Блок 3______) 4.1-«А» Следующая последовательность процедур: 1. Проверка выполнения условий применения данной итерационной схемы. 2. Разделение корней (выделение подобластей, включающих единственный корень) и выбор нулевых приближений для каждой подобласти.. 3. Выполнение итераций, включающих - формулирование линейной задачи - ой итерации; - решение этой задачи с использованием результатов предыдущей итерации (предыдущих итераций); - проверка условий выхода из итерационного цикла; - при выполнении указанных условий – выход из цикла. 4.2- «В» Элемент , удовлетворяющий условию . 4.3.- «В» Множество всех элементов такое, что для любого последовательность принадлежит ей. 4.4- В. Оператор , для которого можно указать постоянную такую, что . 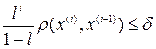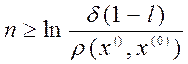4.5- А. Следующая последовательность вычислительных процедур. 1. Проверка возможности использования метода. 2. Выбор начальной точки. 3. Последовательное выполнение итераций, причём любая 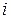- ая итерация выполняется по формуле . 4. Условия выхода из цикла могут иметь следующий вид: , , .    

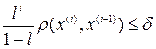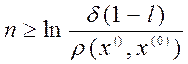А. Следующая последовательность процедур:

1. Проверка выполнения условий применения данной итерационной схемы.

2. Разделение корней (выделение подобластей, включающих единственный корень) и выбор нулевых приближений для каждой подобласти..

3. Выполнение итераций, включающих

- формулирование линейной задачи 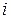- ой итерации;

- решение этой задачи с использованием результатов предыдущей итерации (предыдущих итераций);

- проверка условий выхода из итерационного цикла;

- при выполнении указанных условий – выход из цикла

Дата добавления: 2014-01-20