Тест - контроль для самопроверки. Выход темы в другие темы и дисциплины

Выход темы в другие темы и дисциплины

Данная тема имеет выход в спецкурсы по сопротивлению материалов, строительной механике, строительным конструкциям и механике грунтов, а также в дипломные, магистерские и диссертационные работы.

7.1. Что называется носителем функции?

А. Носителем функции называется достаточно малая подобласть области, на которой задана задача, если:

1) имеется группа координатных функций, для которых она является носителем;

2.) на её границе имеются точки, задание краевых условий (возможно – только главных) в которых однозначно определяет на ней искомую функцию.

Б. Носителем функции называется замыкание области, за пределами которой выполняется условие .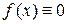

В. Носителем функции называется:

а) для одномерного элемента – один из его концов;

б) для двумерного элемента – одна из точек излома его границы;

в) для трёхмерного элемента – одна из точек излома рёбер (в узле могут встречаться более двух участков рёбер, например, в вершине тетраэдра встречаются три ребра.

Г. Носителями функции называются такие функции 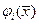в линейной аппроксимации (6.4), (7.1), которые обладают следующими специфическими для МКЭ свойствами:

1) они связаны с одним конкретным узловым параметром одного конкретного узла одного конкретного КЭ данной сетки КЭ;

2) они являются финитными функциями;

3) их носитель – область, занятая данным конкретным КЭ;

4) они равны единице на данном узле, с которым они связаны, и нулю – на остальных узлах донного КЭ;

5) они удовлетворяют специальным требованиям, обеспечивающим совместность КЭ и сходимость конечноэлементных аппроксимаций к точному решению при сгущении сетки.

Кроме того, они удовлетворяют общим требованиям, предъявляемым в прямых методах к координатным функциям.

.

7.2. Что называется финитными функциями?

А. Финитными функциями называются такие функции 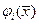в линейной аппроксимации (6.4), (7.1), которые обладают следующими специфическими для МКЭ свойствами:

-они связаны с одним конкретным узловым параметром одного конкретного узла одного конкретного КЭ данной сетки КЭ;

-их носитель – область, занятая данным конкретным КЭ;

-они равны единице на данном узле, с которым они связаны, и нулю – на остальных узлах донного КЭ;

-они удовлетворяют специальным требованиям, обеспечивающим совместность КЭ и сходимость конечноэлементных аппроксимаций к точному решению при сгущении сетки.

Б. Финитными функциями называются коэффициенты линейной аппроксимации свободного члена дифференциального уравнения задачи

В. Финитными функциями называются координатные функции 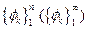, удовлетворяющие определённым требованиям, обеспечивающим сходимость последовательности приближённых решений и повышающих устойчивость процесса счёта.

Г. Финитными функциями называются кусочно-непрерывные функции с ограниченным носителем.

7.3.Что называется конечным элементом?

А. Конечным элементом называется достаточно малая подобласть области, на которой задана задача, если:

1) имеется группа координатных функций, для которых она является носителем;

2.) на её границе имеются точки, задание краевых условий (возможно – только главных) в которых однозначно определяет на ней искомую функцию.

Б. Конечным элементом называется замыкание области, за пределами которой выполняется условие .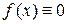

В. Конечным элементом называется

а) для одномерной области – один из её концов;

б) для двумерной области – одна из точек излома её границы;

в) для трёхмерной области – одна из точек излома рёбер её границы.

Г. Конечным элементом называется точка области, в которой совмещены два или более узлов сопрягаемых конечных элементов, а также точка на границе области, где расположен хотя бы один узел КЭ.

7.4.Что называется узлом конечного элемента?

А. Узлом конечного элемента называется точка области, в которой сопрягаются два или более конечных элементов, а также точка на границе области, общая хотя бы с одним КЭ.

Б. Узлом конечного элемента называется замыкание области, за пределами которой выполняется условие .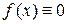

В. Узлом конечного элемента называется:

а) для одномерного элемента – один из его концов;

б) для двумерного элемента – одна из точек излома его границы;

в) для трёхмерного элемента – одна из точек излома рёбер (в узле могут встречаться более двух участков рёбер, например, в вершине тетраэдра встречаются три ребра.

Г. Узлом конечного элемента называется матрица 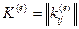, элементы которой определяются по формуле

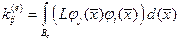
или её аналогу, полученному путём понижения порядка дифференциального оператора.

7.5. Что называется координатными функциями МКЭ?

А. Заранее выбранные в 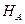(для метода Ритца) и в 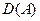(для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.

Б. Заранее выбранные в 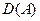(для метода Ритца) и в 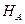(для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.

В. Разность между левой и правой частями дифференциального уравнения задачи.

Г. Координатными функциями МКЭ называются такие функции 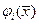в линейной аппроксимации (6.4), (7.1), которые обладают следующими специфическими для МКЭ свойствами:

1) они связаны с одним конкретным узловым параметром одного конкретного узла одного конкретного КЭ данной сетки КЭ;

2) они являются финитными функциями;

3) их носитель – область, занятая данным конкретным КЭ;

4) они равны единице на данном узле, с которым они связаны, и нулю – на остальных узлах донного КЭ;

5) они удовлетворяют специальным требованиям, обеспечивающим совместность КЭ и сходимость конечноэлементных аппроксимаций к точному решению при сгущении сетки.

Кроме того, они удовлетворяют общим требованиям, предъявляемым в прямых методах к координатным функциям

7.6. Что называется матрицей жёсткости конечного элемента?

А. Матрицей жёсткости конечного элемента называется матрица 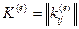, элементы которой определяются поформуле

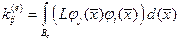
или её аналогу, полученному путём понижения порядка дифференциального оператора.

В случае задач строительной механики МЖ КЭ связывает вектор узловых обобщённых усилий 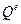с вектором узловых обобщённых перемещений 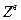формулой

.

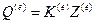Б. Матрицей жёсткости конечного элемента называется матрица 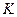коэффициентов разрешающей системы уравнений, вычисляемая по формулам

,

.

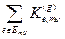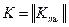Она связывает узловые параметры системы и нагрузку разрешающей системой уравнений.

В. Матрицей жёсткости конечного элемента называется матрица Якоби её узловых параметров, отражающих естественные граничные условия, по узловым параметрам, отражающим главные граничные условия.

Г. Матрицей жёсткости конечного элемента называется матрица значений его координатных функций в его узлах.

7.7. Что называется матрицей жёсткости системы?

А. Матрицей жёсткости системы называется вектор-столбец значений искомой функции в её узлах.

Б. Матрицей жёсткости системы называется вектор-столбец значений свободных членов.

В. Матрицей жёсткости системы называется матрица, устанавливающая соответствие между номерами узлов и номерами КЭ, которым этот узел инцидентен.

Г. Матрицей жёсткости системы называется матрица 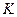коэффициентов её разрешающей системы уравнений, вычисляемая по формулам

,

,

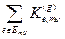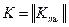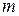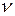где суммирование осуществляется по множеству КЭ, которым инцидентны узлы и , а 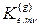- блоки МЖ этих КЭ.

Она связывает главные узловые параметры системы и её естественные узловые параметры (вектор неизвестных со свободным вектором).

7.8. Какой метод прикладной математики реализует метод переменных параметров упругости и в чём он заключается?

А. Метод переменных параметров упругости является реализацией методов дискретного продолжения по параметру нагрузки в сочетании с итерационными методами, уточняющими решение на каждом шаге по нагрузке. Он заключается в том, что в процессе расчёта нагрузка прикладывается достаточно малыми шагами и на каждом шаге выполняется итерационный процесс, в котором в качестве нулевого приближения используется результат расчёта на предыдущем шаге.

Б. Метод переменных параметров упругости - это реализация модифицированного метода Ньютона, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики. Он заключается в пересчёте поправок к МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации, и преобразовании их к поправкам к вектору нагрузок, называемым фиктивными нагрузками. На каждой итерации осуществляется определение вектора неизвестных по сумме действительных и фиктивных нагрузок.

В. Метод переменных параметров упругости - это реализация метода простых итераций, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики.Он заключается в пересчёте МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации.

Г. Метод переменных параметров упругости - это реализация метода продолжения по параметру нагрузки в сочетании с методом секущих. Он заключается в том, что в процессе расчёта нагрузка прикладывается достаточно малыми шагами и на каждом шаге выполняется итерационный процесс метода секущих, в котором в качестве нулевого приближения используется результат расчёта на предыдущем шаге.

7.9. Какой метод прикладной математики реализует метод фиктивных нагрузок и в чём он заключается?

А. Метод фиктивных нагрузок является реализацией методов дискретного продолжения по параметру нагрузки в сочетании с итерационными методами, уточняющими решение на каждом шаге по нагрузке. Он заключается в том, что в процессе расчёта нагрузка прикладывается достаточно малыми шагами и на каждом шаге выполняется итерационный процесс, в котором в качестве нулевого приближения используется результат расчёта на предыдущем шаге.

Б. Метод фиктивных нагрузок - это реализация модифицированного метода Ньютона, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики. Он заключается в пересчёте поправок к МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации, и преобразовании их к поправкам к вектору нагрузок, называемым фиктивными нагрузками. На каждой итерации осуществляется определение вектора неизвестных по сумме действительных и фиктивных нагрузок.

В. Метод фиктивных нагрузок - это реализация метода простых итераций, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики.Он заключается в пересчёте МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации.

Г. Метод фиктивных нагрузок - это реализация метода продолжения по параметру нагрузки в сочетании с методом секущих. Он заключается в том, что в процессе расчёта нагрузка прикладывается достаточно малыми шагами и на каждом шаге выполняется итерационный процесс метода секущих, в котором в качестве нулевого приближения используется результат расчёта на предыдущем шаге.

7.10. Какие методы прикладной математики реализуют шагово-итерационные методы и в чём они заключаются?

А. Шагово-итерационные методы являются реализацией методов дискретного продолжения по параметру нагрузки в сочетании с итерационными методами, уточняющими решение на каждом шаге по нагрузке. Они заключаются в том, что в процессе расчёта нагрузка прикладывается достаточно малыми шагами и на каждом шаге выполняется итерационный процесс тем или иным итерационным методом, в котором в качестве нулевого приближения используется результат расчёта на предыдущем шаге.

Б. Шагово-итерационные методы - это реализация модифицированного метода Ньютона, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики. Они заключаются в пересчёте поправок к МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации, и в использовании их для вычисления поправок к вектору нагрузок, называемых фиктивными нагрузками. На каждой итерации осуществляется определение вектора неизвестных по сумме действительных и фиктивных нагрузок.

В. Шагово-итерационные методы - это реализация метода простых итераций, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики.Они заключаются в пересчёте МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации.

Г. Шагово-итерационные методы - это реализация метода продолжения по параметру нагрузки в сочетании с методом секущих. Они заключаются в том, что в процессе расчёта нагрузка прикладывается достаточно малыми шагами и на каждом шаге выполняется итерационный процесс метода секущих, в котором в качестве нулевого приближения используется результат расчёта на предыдущем шаге.

7.1. «Б» - Б. Носителем функции называется замыкание области, за пределами которой выполняется условие .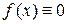

7.2. «Г» - Финитными функциями называются кусочно-непрерывные функции с ограниченным носителем.

7.3. «А» - Конечным элементом называется достаточно малая подобласть области, на которой задана задача, если:

1) имеется группа координатных функций, для которых она является носителем;

2.) на её границе имеются точки, задание краевых условий (возможно – только главных) в которых однозначно определяет на ней искомую функцию.

7.4. «В» - Узлом конечного элемента называется:

а) для одномерного элемента – один из его концов;

б) для двумерного элемента – одна из точек излома его границы;

в) для трёхмерного элемента – одна из точек излома рёбер (в узле могут встречаться более двух участков рёбер, например, в вершине тетраэдра встречаются три ребра.

?.5. «Г» - Координатными функциями МКЭ называются такие функции 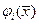в линейной аппроксимации (6.4), (7.1), которые обладают следующими специфическими для МКЭ свойствами:

1) они связаны с одним конкретным узловым параметром одного конкретного узла одного конкретного КЭ данной сетки КЭ;

2) они являются финитными функциями;

3) их носитель – область, занятая данным конкретным КЭ;

4) они равны единице на данном узле, с которым они связаны, и нулю – на остальных узлах донного КЭ;

5) они удовлетворяют специальным требованиям, обеспечивающим совместность КЭ и сходимость конечноэлементных аппроксимаций к точному решению при сгущении сетки.

Кроме того, они удовлетворяют общим требованиям, предъявляемым в прямых методах к координатным функциям.

7.6. «А».- Матрицей жёсткости конечного элемента называется матрица 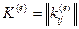, элементы которой определяются поформуле

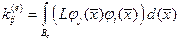
или её аналогу, полученному путём понижения порядка дифференциального оператора.

В случае задач строительной механики МЖ КЭ связывает вектор узловых обобщённых усилий 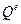с вектором узловых обобщённых перемещений 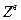формулой

.

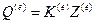7.7. «Г» -. Матрицей жёсткости системы называется матрица 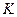коэффициентов её разрешающей системы уравнений, вычисляемая по формулам

,

,

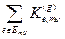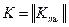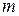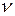где суммирование осуществляется по множеству КЭ, которым инцидентны узлы и , а 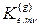- блоки МЖ этих КЭ.

Она связывает главные узловые параметры системы (вектор неизвестных) и её естественные узловые параметры (свободный вектор).

7.8. «В» - Метод переменных параметров упругости - это реализация метода простых итераций, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики.Он заключается в пересчёте МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации.

7.9. «Б» -. Метод фиктивных нагрузок - это реализация модифицированного метода Ньютона, ориентированная на решение задач механики деформируемого твёрдого тела и, прежде всего,- строительной механики. Он заключается в пересчёте поправок к МЖ на каждой итерации по секущим модулям, определённым по деформациям предыдущей итерации, и преобразовании их к поправкам к вектору нагрузок, называемым фиктивными нагрузками. На каждой итерации осуществляется определение вектора неизвестных по сумме действительных и фиктивных нагрузок.

7.10. «А».- Шагово-итерационные методы являются реализацией методов дискретного продолжения по параметру нагрузки в сочетании с итерационными методами, уточняющими решение на каждом шаге по нагрузке. Они заключаются в том, что в процессе расчёта нагрузка прикладывается достаточно малыми шагами и на каждом шаге выполняется итерационный процесс тем или иным итерационным методом, в котором в качестве нулевого приближения используется результат расчёта на предыдущем шаге.

.

Дата добавления: 2014-01-20