Метод стрельб

Тематическое содержание.

Содержание темы.

Входная информация для самопроверки

ММ-9. Ключевые слова и понятия

ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА.

ММ-9. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ РЕШЕНИЯ

9.1. Собственное значение дифференциального оператора.

9.2. Собственное решение дифференциального оператора.

9.3. Метод стрельб.

9.4. Фазовый метод.

9.5. Разностный метод.

9.6. Метод дополнительного вектора.

9.7. Метод Галеркина.

Для изучения данной темы Вам необходимо восстановить в памяти:

:- из курса прикладной математики- решение однородного дифференциального уравнения с постоянными коэффициентами, в случае, когда его характеристическое уравнение имеет комплексно-сопряженные корни; определение собственного значения и собственной функции дифференциального уравнения, полная система ортогональных функций;

- из настоящего спецкурса – ортогональные функции.

9.2.1. Структурно – логическая схема содержания темы

К чимслу задач сопротивления материалов,помимо расчетов на прочность и жесткость, относятся также расчеты на устойчивость. Расчет на устойчивость имеет первостепенное значение для тех элементов конструкций, которые представляют собой сравнительно длинные и тонкие стержни, тонкие пластины и оболочки.

В механике равновесие называют устойчивым, если при любом малом отклонении от положения равновесия тело возвращается в исходное положение при устранении причины, вызывающей это отклонение. Равновесие называют неустойчивым, если при любом малом отклонении от положения равновесия тело не возвращается в исходное положение, а все далее отклоняется от него.

В сопротивлении материалов, т.е. в механике деформируемого тела, основным является установление зависимости вида равновесия от величины сил, действующих на элемент конструкции.

Рассмотрим сравнительно длинный и тонкий прямолинейный стержень длиной l. Стержень защемлен одним концом, а другой конец стержня свободен. На свободный конец в центре тяжести концевого сечения действует сжимающая сила 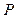, направленная вдоль оси стержня. Допустим, что главные оси инерции всех сечений стержня лежат в двух фиксированных направлениях.

Рис. 9.1. Продольный изгиб стержня, защемленного на одном конце и свободного на другом.

Если приложить к стержню поперечную нагрузку, т.е. слегка изогнуть его, то при малых значениях сжимающей силы после снятия поперечной нагрузки стержень вернется в прямолинейное состояние. Это значит, что прямолинейная форма равновесия оси стержня устойчива. При большем значении сжимающей силы слегка изогнутый поперечной нагрузкой стержень после ее устранения “ медленнее “ возвращается в прямолинейное положение. Но всеже прямолинейная форма равновесия еще устойчива. Наконец, при некотором значении сжимающей силы прямолинейная форма равновесия оси стержня становится неустойчивой и возникает новая устойчивая форма равновесия – криволинейная. Происходит выпучивание стержня. Существенно, что при достижении сжимающей силы того значения (критического), при котором прямолинейная форма равновесия оси стержня становится неустойчивой, для перехода к криволирейной форме нет надобности прикладывать к стержню поперечную нагрузку, и изгиб стержня происходит без видимых внешних причин. Изгиб стержня, связанный с потерей устойчивости прямолинейной формы его равновесия, называют продольным изгибом.

Рассмотрим вопрос о велечине критической силы сжатого стержня один конец которого защемлен, а второй свободен (рис. 9.1). Пусть стержень находится в несколько изогнутом состоянии. На рис. 9.1 это положение изображено пунктирной линией.

Упругой линией (кривой изгиба) в сопротивлении материалов называется кривая y=f(z), которую принимает нейтральный слой, т.е. слой, в котором волокна стержня не деформируются (не растягиваются и не сжимаются) под действием сил. Прогибом стержня называется ордината упругой линии в рассматриваемом сечении.

Выберем систему координат, как показано на рис.9.1. Из курса сопротивления материалов известно, что радиус кривизны ρ упругой линии для стержня любого сечения равен:

,

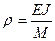где E – модуль упругости стержня, J – момент инерции поперечного сечения стержня относительно нейтральной оси (нейтральная ось – прямая пересечения нейтрального слоя с плоскостью данного сечения), M – изгибающий момент для данного сечения, равный алгебраической сумме моментов относительно нейтральной оси всех внешних сил, приложенных к стержню. Так как изгибы стержней обычно малы, то упругая линия мало отклоняется от оси z и в любой ее точке угловой коэффициент касательной y′(z) весьма мал. Поэтому в выражении для радиуса кривизны

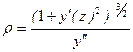
величиной 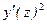можно пренебречь и для упругой линии получим дифференциальное уравнение

.

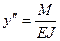В рассматриваемом случае абсолютная величина изгибающего момента в произвольном сечении стержня равна 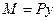и дифференциальное уравнение изогнутой оси стержня имеет вид:

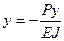. (9.1)

Знак минус поставлен потому, что независимо от выбора положительного направления оси O y

Знаки кривизны 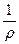и ординаты прогиба y противоположны.

Рассмотрим случай постоянного поперечного сечения EJ=const и положим 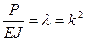. Тогда дифференциальное уравнение (9.1) примет вид:

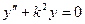. (9.2)

Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение имеет пару комплексно-сопряженных корней 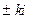и решение уравнения (9.2) имеет вид:

,

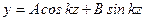где A и B – постоянные интегрирования, которые определяются из граничных условий.

Рассмотрим граничные условия, которые зависят от способа закрепления стержня и в данном случае они имеют вид:

, .

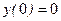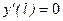. Из условия 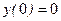следует, что А=0. Второе граничное условие дает

.

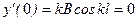От сюда следует три случая:

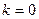1. , то есть P =0 - нагрузка отсутствует;
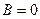2. , тогда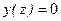. Это решение соответствует прямолинейному положению равновесия;

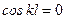1. , то есть. Данным значениям k соответствуют критические нагружения

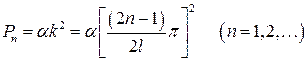
и каждому из этих специальных значений соответствует определенная функция прогиба .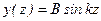

Таким образом, математически задача формулируется в следующем виде: рассматривается линейное однородное дифференциальное уравнение

с однородными граничными условиями 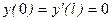. Требуется найти такие значения 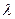, при которых задача имеет нетривиальное решение. Эти значения называются собственными значениями и для каждого собственного значения есть собственная функция .

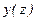К подобного рода проблемам приводятся задачи: о продольно сжатом стержне на упругом основании; о потере устойчивости консольной балки при изгибе; о сжатии и кручении вала; о выпячивании круговой арки; об изгибных колебаниях стержня; о крутильных колебаниях диска и т.д.

Если объединить выше перечислены примеры, то можно сформулировать математическую задачу на собственные значения дифференциального уравнения в следующем виде.

Рассматривается дифференциальное уравнение вида

где 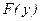и G(y) – линейно- однородные обыкновенные дифференциальные уравнения вида

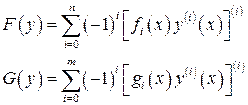
и 2 n линейных однородных относительно значений y и ее производных в двух фиксированных точках a и b граничных условия

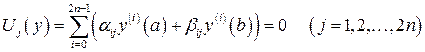
где 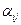и 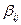действительные, не равные нулю одновременно постоянные. Граничные условия должны быть линейно-независимые. Требуется определить, при каких значениях 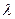эта задача имеет не нулевое решение.

В частности, при n=1, 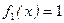, m =0, 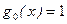, j =2, a= 0, b=l, 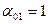, , 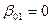, , 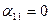, , 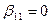, 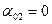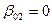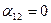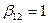имеем классическую задачу о продольном изгибе упругого стержня, защемленного на одном конце.

На практике аналитическое решение поставленной задачи очень сложно получить. Поэтому рассмотрим наиболее часто употребляемые численные методы решения задачи на собственные значения и собственные решения.

Основные черты этого метода рассмотрим для случая n= 1 и граничных условиях вида 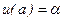и 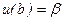. Если отбросить второе граничное условие и выбрать некоторое значение параметра 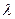, то начальная задача превращается в задачу Коши. Численно интегрируя ее, получим решение, которое удовлетворяет первому краевому условию. В целом 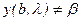, то есть это решение не удовлетворяет второму граничному условию. Тогда, изменяя 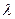, добьемся того, что 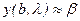с необходимой точностью. Таким образом, задача сводится к задаче Коши и решению алгебраического уравнения. Если 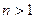, то в качестве начальных условий для задачи Коши берут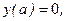 , …, 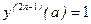и ведут пристрелку параметра 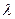до выполнения 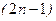граничных условий, которые остаются.

Этот метод трудно применять, если задача Коши плохо обусловленна, то есть когда малые изменения параметра 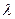резко меняют решение .

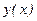Дата добавления: 2014-01-20