Решение двойственных задач

Лекция 5

Решение симметричных задач

Рассмотрим решение задач с использованием теорем двойственности.

Исходная задача

при ограничениях:

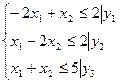
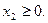
Двойственная задача

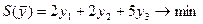
при ограничениях:

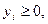
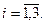
Решим исходную задачу графическим методом, получим 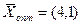, при этом

На основании 1-й теоремы двойственности

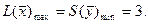
Так как 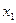, 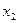>0, то по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств: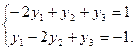

Подставим 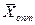в систему ограничений исходной задачи:

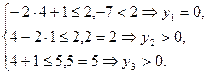
Тогда система ограничений двойственной задачи примет вид

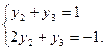
Откуда , при этом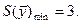

Пусть дано решение двойственной задачи , , 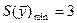найдём решение исходной.

По 1-й теореме двойственности 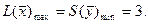Так как , 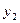>0, то по 2-й теореме двойственности второе и третье неравенства исходной задачи обращаются в равенства:

Откуда 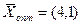, при этом

Рассмотрим решение задач методом, основанным на взаимно однозначном соответствии между переменными: основным переменным исходной задачи соответствуют балансовые переменные двойственной, и наоборот. Для этого решим двойственную задачу симплексным методом:

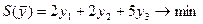
при ограничениях:

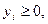
bj	БП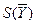
y1	y2	y3	y4	y5	cj
		-2	-2		-1	-1	-1

bj	БП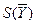
y1	y2	y3	y4	y5	cj
	y2	-2 -3			-1 -2	-1

bj	БП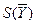
y1	y2	y3	y4	y5	cj
	y2 y3	-1 -1			-1/3 -2/3	1/3 -1/3	2/3 1/3
∆i	-9			-4	-1

, .

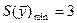На основании 1-й теоремы двойственности получаем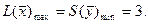

Решение другой задачи найдём по соответствию между переменными:

	Основные переменные	Балансовые переменные
Исходная задача	x1 x2	x3 x4 x5
Двойственная	y4 y5	y1 y2 y3
	Балансовые переменные	Основные переменные

Значение x_j определяем по последней симплексной таблице в строке ∆_i в соответствующем столбце, причём значения x_j берутся по модулю:.

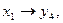
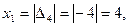
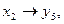
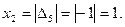
Таким образом, решение двойственной задачи:

, .

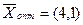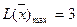Если исходная задача решена симплексным методом, то решение двойственной задачи может быть найдено по формуле 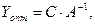где С – матрица-строка коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи; А^-1 – обратная матрица для матрицы А, являющейся матрицей коэффициентов системы ограничений исходной задачи для базисных переменных в оптимальном решении.:

при ограничениях:

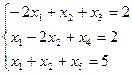
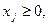
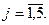
сi	БП		-1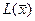
х1	х2	х3	х4	х5	bi
	x3 x4 x5	-2	-2
∆j	-1

сi	БП		-1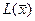
х1	х2	х3	х4	х5	bi
	x3 x1 x5		-3 -2		-1
∆j		-1

сi	БП		-1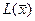
х1	х2	х3	х4	х5	bi
-1	x3 x1 x2				1/3 -1/3	2/3 1/3
∆j				2/3	1/3

Из табл. следует, что 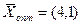, при этом

Матрицы записываются в виде

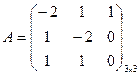, , тогда .

=.

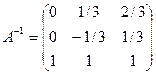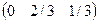Таким образом, решение двойственной задачи следующее: , .

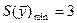Решение несимметричных задач

Рассмотрим решение задач с использованием теорем двойственности.

Исходная задача

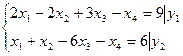
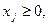
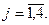
Двойственная задача

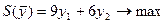
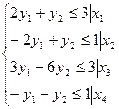
у₁, у₂ – произвольные по знаку.

Решив двойственную задачу графическим методом, получим

, при этом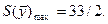

По 1-й теореме двойственности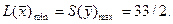

Подставим 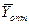в систему ограничений двойственной задачи:

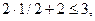3=3,

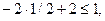1=1,

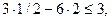-21/2<3 ,

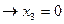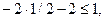-3<1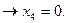

Так как х₃ = х₄ = 0, то система исходной задачи примет вид

Решая данную систему, получим , при этом

Рассмотрим решение задач с использованием обратной матрицы.

Пусть решение исходной задачи , при этом

Решение двойственной задачи найдём по формул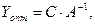е где

, , =.

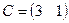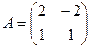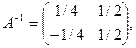
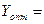
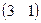
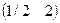Таким образом, , .

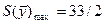Решение смешанных двойственных задач

Смешанные двойственные задачи можно решать с использованием теорем двойственности.

Исходная задача

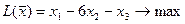
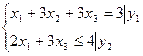
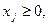
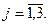
Двойственная задача

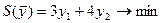
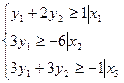
у₁ – произвольная по знаку,

у₂

Найдём оптимальное решение двойственной задачи, решив сначала исходную симплексным методом:

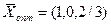, при этом

По 1-й теореме двойственности

Так как х₁ > 0, x₃ > 0, то по 2-й теореме двойственности первое и третье ограничения двойственной задачи выполняются в виде равенств: ,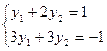

откуда у₁ = -5/3, у₂ = 4/3, т. е.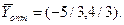

Дата добавления: 2014-01-11